Base de Ker(f)

[Syphax]

N'ayant pas fait d'algèbre depuis un an presque, on m'a demandé de faire un ptit exo d'algèbre linéaire. Et, en lisant la correction de cet exo, je n'ai pas très bien compris.

On a f : Rn[X] -> Rn[X]
P -> P + (1+X)*P'

Donner une base de Ker(f).

Au final, je suis bien arrivé, comme dans le corrigé, à P=a1*X- a1= a1(X-1).
Ils concluent alors par Ker(f)=Vect(X-1). Moi, j'aurai plutôt mis Vect({1,X}) vu que P s'écrit comme a*1 + b*X et 1 et X sont des élèments de la base de Rn.
On doit bien écrire Ker(f) avec des élèments de l'ensemble de départ (ici Rn), non ?

[Manny06]

N'ayant pas fait d'algèbre depuis un an presque, on m'a demandé de faire un ptit exo d'algèbre linéaire. Et, en lisant la correction de cet exo, je n'ai pas très bien compris.

On a f : Rn[X] -> Rn[X]
P -> P + (1+X)*P'

Donner une base de Ker(f).

Au final, je suis bien arrivé, comme dans le corrigé, à P=a1*X- a1= a1(X-1).
Ils concluent alors par Ker(f)=Vect(X-1). Moi, j'aurai plutôt mis Vect({1,X}) vu que P s'écrit comme a*1 + b*X et 1 et X sont des élèments de la base de Rn.
On doit bien écrire Ker(f) avec des élèments de l'ensemble de départ (ici Rn), non ?

attention a(X-1) n'est pas la même chose que a*1+b*X
les coefficients de 1 et X doivent être opposés

[Anonyme]

@Syphax

Il doit y avoir une erreur de signe quelque part dans ton énoncé ? (une faute de frappe ?)

car si on pose P(x)=a1(x-1)

alors P'(x)=a1 et on a P(x) + (1+x)*P'(x) = a1(x-1) + a1(1+x)= 2a1 x et donc
.

[Syphax]

Ah oui, j'ai fait une erreur : P -> P+(1 - X) * P' et non (1 + X).

Mais, X-1 n'appartient pas à la base de Rn, non ? Par contre, 1 et X si.

[Anonyme]

@Syphax

- Les n+1 polynômes définis par lorsque 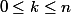forment une base de l'E.V. des polynômes réels à une variable réelle et de puissance inférieure ou égale à n

- Les n+1 polynômes définis par lorsque 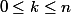forment une AUTRE base de l'E.V. des polynômes réels à une variable réelle et de puissance inférieure ou égale à n

[Syphax]

@Syphax

- Les n+1 polynômes définis par lorsque forment une base de l'E.V. des polynômes réels à une variable réelle et de puissance inférieure ou égale à n

- Les n+1 polynômes définis par lorsque forment une AUTRE base de l'E.V. des polynômes réels à une variable réelle et de puissance inférieure ou égale à n

Ah ok.
Mais en quoi la base que j'ai donné est fausse ? Je ne vois pas où est mon erreur.

[Anonyme]

@Syphax

L' E.V. Vect({1,X}) est de dimension 2

alors que L' E.V. Vect({1+X}) est de dimension 1

[Anonyme]

@Syphax

Question supplémentaire :
Comment démontre-t-on que les n+1 polynômes définis par lorsque forment une base de l'E.V. des polynômes réels à une variable réelle et de puissance inférieure ou égale à n ?