Devoir prépa CAPES

[ROM_CAPES]

Bonjour, voilà donc je ne suis pas sûr d'une réponse à une question, j'aimerais savoir ce que vous en pensez.

Enoncé

Rappels de notations :
f est une application de I vers avec I un intervalle de
On considère l'équation :
E(I) : avec f dérivable sur I
On note S(I) l'ensemble des solutions de l'équation E(I)

Dans cette question, on suppose que I =
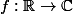
On considère une application développable en série entière au point 0 ; il existe donc un réel strictement positif, noté R, ainsi qu'une suite complexe , tels que et
,


Question : Montrer que : si alors f est polynomiale sur ]-R, R[ puis sur


Ma redaction

Supposons que
Alors,



f étant dérivable sur ]-R,R[ on a :

donc,

On a donc : ie
ie

On doit donc avoir ,
Auparavant, on a déjà étudié l'application et on a montré notamment que l'ensemble des solutions de l'équation ,d'inconnue réelle t , est l'ensemble {1,2}

On doit donc avoir nécessairement ici {1,2}.

Si , alors , où et donc f est polynomiale sur ]-R, R[ et même sur (evident)

Merci de m'éclairer sur les erreurs que j'ai pu faire :id:

ROM :++:

[quinto]

donc f est polynomiale sur ]-R, R[ et même sur (evident)

Pourquoi c'est évident?

[ROM_CAPES]

oups oui c'est sût ça ne l'est pas mais je ne sais pas comment le justifier :hein:

[kms040584]

Salut,
j'ai regarde rapidement ta réponse, mais j'ai une remarque, ton passage

à 'on doit donc avoir....' me semble louche...ne vaut t'il pas mieux parler d'unicité de développement en série entière?
++

[quinto]

oups oui c'est sût ça ne l'est pas mais je ne sais pas comment le justifier :hein:

Tu dis que c'est évident, mais tu ne sais pas le justifier, c'est drôle...
Tu sais qu'en oral ça t'aurais fait très mal ...

Que peux tu dire de deux fonctions développables en série entière et égales sur un ensemble possédant un point d'accumulation?

[ROM_CAPES]

:triste:

Je connais ce résultat que j'avais vu en analyse complexe cette année.
Si f est un développement en série entière sur un domaine U de et si Z(f) = {} admet un point d'accumulation dans U alors f est nulle au voisinage de a

[quinto]

Je connais ce résultat que j'avais vu en analyse complexe cette année.
Si f est un développement en série entière sur un domaine U de et si Z(f) = {} admet un point d'accumulation dans U alors f est nulle au voisinage de a

Ce n'est pas le résultat dont je parle (bien qu'il puisse s'en déduire).
Si deux séries entières sont égales sur un ensemble possèdant un point d'accumulation, alors elles sont égales partout.
C'est le principe d'identité.

Ca te dit qu'il y'a un genre de manque de souplesse pour les fonctions développables en série entière. Tu ne peux pas faire n'importe quoi avec une fonction développable en série entière, en ce sens que si tu fixes quelque points, tu as fixé toutes ses valeurs.

En fait, je pense que l'on aurait facilement conclu sans ce résultat, mais avec un peu de calculs.
a+

[ROM_CAPES]

On a donc : ie
ie

On doit donc avoir ,

J'ai du mal avec ce passage, je ne sais pas comment le rédiger

Quinto merci pour ton aide ça m'a bien aidé, je ne sais pas si j'avais deja vu ce résultat quoique j'ai du l'oublier :hum:

[ROM_CAPES]

il faut peut être exprimer cette série en série de Taylor plutôt non?

Théorème : Soit f développable en série entière à l'origine, alors f est de classe au voisinage de 0, et cette série entière est la série de Taylor :

merci

[kms040584]

J'ai du mal avec ce passage, je ne sais pas comment le rédiger

Quinto merci pour ton aide ça m'a bien aidé, je ne sais pas si j'avais deja vu ce résultat quoique j'ai du l'oublier :hum:

Salut, normalement il n'y pas trop de redaction pour cette partie. Tu ecris ton égalité, tu passes la partie de droite a gauche, puis sous le même signe somme, et ensuite tu as Somme ( ) = 0 or 0 est bien developpable en série entière avec tous les "an" égaux a 0. Ce developpement, s'il existe (ici c'est le cas), est unique. Donc tous les "an" de gauche sont egaux aux "an" de la fonction nulle, qui sont justement nuls. Donc pour tout n, an de gauche = 0
voila, je sais pas si c'etait la ton pb
a plus
K.

[quinto]

Salut,
si c'est un polynôme de degré n sur (-R,R) R>0, dérive n+1 fois et tu as la fonction nulle.
Ainsi ta série (dérivée n-ieme) est nulle sur un ouvert non vide, donc est nulle partout, et donc ta fonction de départ est un polynôme de degré au plus n (en fait on peut montrer que c'est exactement n)

[ROM_CAPES]

Salut, normalement il n'y pas trop de redaction pour cette partie. Tu ecris ton égalité, tu passes la partie de droite a gauche, puis sous le même signe somme, et ensuite tu as Somme ( ) = 0 or 0 est bien developpable en série entière avec tous les "an" égaux a 0. Ce developpement, s'il existe (ici c'est le cas), est unique. Donc tous les "an" de gauche sont egaux aux "an" de la fonction nulle, qui sont justement nuls. Donc pour tout n, an de gauche = 0
voila, je sais pas si c'etait la ton pb
a plus
K.

mais tous les ne sont pas nuls, en fait on trouve bien que les sont nuls pour \{1,2}

si f est développable en série entière au point 0, alors il existe tels que f(x) = ax + bx² pour

Oui en fait le point délicat de cette question se situe dans montrer que f est polynomiale sur mais Quinto m'a donné une méthode

merci! :++:

[quinto]

slt . Si g bien lu la question posée je pense qu on doit monter ceci : si F est solution de l equa donée... implque que F est développable en séries entiéres au vois de 0 .

Moi j'ai lu: "supposons f DES, alors montrer que ...."
ce qui n'est pas du tout la même chose que ce que tu dis.
Peut être parles tu d'une autre question.