Equation 2nd degrés_Equation Cartesienne_ Parabole

[mcar0nd]

Ha j'y arrive pas j'en ai marre jsuis vraiment nul !!

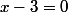
Mais non, tu sais que donc ça veut dire que et ça tu peux le résoudre.

[louise83]

Ha mais je savais pas qu'on pouvais enlever les parenthese et le carré comme sa ! x=3 ?

[mcar0nd]

Ha mais je savais pas qu'on pouvais enlever les parenthese et le carré comme sa ! x=3 ?

Ba .
Donc oui, la solution c'est .

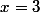
[louise83]

Ha ok j'ai compris !! :) mais on en fait quoi du 2 qu'il y avais avant la parenthèse ?

[mcar0nd]

Ha ok j'ai compris !! mais on en fait quoi du 2 qu'il y avais avant la parenthèse ?

Ba il est facteur de donc pour que ce soit égal, il ne peut que y avoir que qui soit égal à zéro.
C'est un produit, et pour que ça soit égal à 0, il faut que l'in au moins des produits soient égal à 0, or 2 est différent de 0 donc tu ne peux avoir que .

[louise83]

Oui c'est bien ce que je me disais :) Donc la on a fait la resolution de 2(x-3)²+14;)14 ? Mais pour 2(x-3)²+14=14 on fais comment ? (je vais mettre un peut longtemps a repondre parce que je vais manger mais je revien juste après, a tte :) )

[mcar0nd]

Oui c'est bien ce que je me disais Donc la on a fait la resolution de 2(x-3)²+14;)14 ? Mais pour 2(x-3)²+14=14 on fais comment ? (je vais mettre un peut longtemps a repondre parce que je vais manger mais je revien juste après, a tte )

Non là, on vient de résoudre .

[mcar0nd]

OK, a toute.

[louise83]

Heu oui c'est ce que je voulais dire ^^ mais donc pour l'autre on fait comment ?

[mcar0nd]

Heu oui c'est ce que je voulais dire ^^ mais donc pour l'autre on fait comment ?

Pour la a), 2(x-3)^2+14 >= 14
2(x-3)^2 >=0
Donc ça c'est toujours vrai puisqu'un carré, ici (x-3)^2 est toujours positif et il est multiplié par 2>0 donc il garde sa positivité.
Qu'est ce que ça veut dire ta fonction f est toujours supérieure ou égale à 14?

[louise83]

Qu'elle va pas en dessous de 14 donc on exclus tout les resultats en dessous de 14 ?

[mcar0nd]

Qu'elle va pas en dessous de 14 donc on exclus tout les resultats en dessous de 14 ?

Alors elle va pas en dessous de 14 c'est vrai mais on exclut les résultats en dessous de 14.
Si elle ne vas pas en dessous de 14, ça veut dire que 14 est son minimum, c'est la "plus petite" image de la fonction pour x de [0;4].

[louise83]

Ha ok et donc comment on procède pour arriver a la résoudre ?

[mcar0nd]

Ha ok et donc comment on procède pour arriver a la résoudre ?

Tu la résous pas, tu montre qu'elle est vraie pour tout x appartenant à l'intervalle [0;4].

[louise83]

Ha ok et on fais comment du coup ? :)

[mcar0nd]

Ha ok et on fais comment du coup ?

Comme je t'ai dit tout à l'heure.
, ce qui est vrai car comme c'est un carré (et qu'un carré est toujours positif) et la multiplication par 2 conserve cette positivité.

[louise83]

Ok merci :) donc la j'ai bien terminé ? :)

[mcar0nd]

Ok merci donc la j'ai bien terminé ?

Oui, il te reste à répondre à la c).

Tu sais que le minimum de la fonction est 14 (c'est une image)(d'après la question a) et qu'il atteint en x=3 (c'est un antécédent)(d'après la question b).

Tu en conclus donc quoi quant au coordonnées de ce minimum? Elles valent quoi?

[louise83]

Elles valent (3;14) ? :)

[mcar0nd]

Elles valent (3;14) ?

Exactement.
Et la forme canonique c'est ça . Tu t'aperçois donc que ton minimum a pour coordonnées soit .
Et là c'est terminé.