Bonjour
Je voulais savoir s'il existe des formules pour simplifier des expressions du genre:
A=V[9+4V(5)]
B=V[23-6V(14)]
V=racine carrée
Merci
Racines imbriquées
11 messages
- Page 1 sur 1
kadaid a écrit:Bonjour
Je voulais savoir s'il existe des formules pour simplifier des expressions du genre:
A=V[9+4V(5)]
B=V[23-6V(14)]
V=racine carrée
Merci
pour A tu peux essayer de trouver a et b tels que (a+b
tu tombes sur
a²+5b²=9
ab=2
en multipliant de chaque côté la première égalité par a², tu as
tu poses A=a²
il faut résoudre A²-9A+20=0
ce qui donne A=5 et A=4
parmi les solutions (a,b)=(2,1)
Bonjour
Je voulais revenir un peu en arrière
Pour le A, j'ai remarqué qu'en factorisant par 4, alors le coefficient de V(5) est 1 et on cherche un seul réel a tel que 4[9/4+V(5)] = (a+V(5))^2
On arrive à a=2 ou a=-2 et finalement A=V[9+4V(5)] = 2+V(5)
Malheureusement cela ne marche pas pour B, je ne sais pas pourquoi.
Autre chose: pour l'identification, est ce que c'est un cas général par exemple E + F = 0, alors
E=0 ET F=0
Si on prend x^2 + x -1=0 et si je pose
x^2=0 et x-1=0, et bien 0 et 1 ne sont pas solutions. Ou peut être je mélange des choses...
Merci
Je voulais revenir un peu en arrière
Pour le A, j'ai remarqué qu'en factorisant par 4, alors le coefficient de V(5) est 1 et on cherche un seul réel a tel que 4[9/4+V(5)] = (a+V(5))^2
On arrive à a=2 ou a=-2 et finalement A=V[9+4V(5)] = 2+V(5)
Malheureusement cela ne marche pas pour B, je ne sais pas pourquoi.
Autre chose: pour l'identification, est ce que c'est un cas général par exemple E + F = 0, alors
E=0 ET F=0
Si on prend x^2 + x -1=0 et si je pose
x^2=0 et x-1=0, et bien 0 et 1 ne sont pas solutions. Ou peut être je mélange des choses...
Merci
Salut,
si en fait ça marche aussi :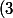^2+(-\sqrt{14})^2+2 \cdot 3 \cdot (-\sqrt{14}))
En général non our tout x, x + (-x) = 0, mais x n'est pas forcément égal à 0.
our tout x, x + (-x) = 0, mais x n'est pas forcément égal à 0.
L'équation x^2 + x -1=0 n'est pas équivalente au système (x^2=0 et x-1=0).
kadaid a écrit:Malheureusement cela ne marche pas pour B, je ne sais pas pourquoi.
si en fait ça marche aussi :
kadaid a écrit:Autre chose: pour l'identification, est ce que c'est un cas général par exemple E + F = 0, alors
E=0 ET F=0
En général non
kadaid a écrit:Si on prend x^2 + x -1=0 et si je pose
x^2=0 et x-1=0, et bien 0 et 1 ne sont pas solutions. Ou peut être je mélange des choses...
Merci
L'équation x^2 + x -1=0 n'est pas équivalente au système (x^2=0 et x-1=0).
kadaid a écrit:Bonjour Luc
Pour trouver a et b à partir de (a+bV(5) )²=9+4V(5)
a^2+2abV(5)+5b^2 = 9+4V(5)
Pourquoi on pose:
a^2+5b^2=9 et 2ab=4
Comment on raisonne ?
Merci
Quand tu as une égalité de la forme
Tu peux "identifier" en disant que le coefficient devant la racine correspond au coefficient qui se trouve de l'autre côté de l'égalité.
Tu peux faire la même chose avec les polynomes
ax² + bx + c = 3x² + 2x + 4 => a = 3, b = 2, c = 4
Donc c'est pour cette raison qu'on pose
a²+5b²=9 et 2ab=4
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
