Intégrale

[prepsain]

Bonjour,

Je coince un peu sur cet exo:

soit de non identiquement nulle telle que

Montrer que s'annule au moins fois sur

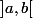
j'ai essayé de raisonner par l'absurde mais ..

[arnaud32]

Bonjour,

Je coince un peu sur cet exo:

soit de non identiquement nulle telle que

Montrer que s'annule au moins fois sur

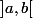
j'ai essayé de raisonner par l'absurde mais ..

t'as pas une hypothese de regularite sur f?

[prepsain]

t'as pas une hypothese de regularite sur f?

Si f est continue et non identiquement nulle sur

[Maxmau]

Bonjour,

Je coince un peu sur cet exo:

soit de non identiquement nulle telle que

Montrer que s'annule au moins fois sur

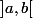
j'ai essayé de raisonner par l'absurde mais ..

L'hyp implique Integ de Pf =0 pour tout polynome de degre inferieur a n
Par l'absurde essaie de trouver un polynome Q de degre inferieur a n fq Qf >=0

[prepsain]

L'hyp implique Integ de Pf =0 pour tout polynome de degre inferieur a n
Par l'absurde essaie de trouver un polynome Q de degre inferieur a n fq Qf >=0

Oui justement mais je n'arrive pas a faire la démo

[SimonB]

Tu connais les polynômes de Lagrange ?

[prepsain]

Tu connais les polynômes de Lagrange ?

Non et je ne vois pas ou est le rapport!

[SimonB]

Effectivement, j'ai dit un peu n'importe quoi, c'est plus simple.

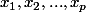
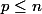
Si f s'annule moins de n fois sur [a,b], tu peux dresser son tableau de signe (en appelant ses zéros , . Cherche alors à construire un polynôme P tel que P*f ait un signe constant.

[prepsain]

Effectivement, j'ai dit un peu n'importe quoi, c'est plus simple.

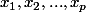
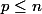
Si f s'annule moins de n fois sur [a,b], tu peux dresser son tableau de signe (en appelant ses zéros , . Cherche alors à construire un polynôme P tel que P*f ait un signe constant.

La piste est de raisonner par l'absurde mais a savoir f s'annule au plus n-2 fois (si j'ai bien compris) mais je ne vois pas par ou aller, j'ai essayé d'écrire l'integrale sous forme d'une somme mais ça ne mène nul part

[SimonB]

La piste est de raisonner par l'absurde mais a savoir f s'annule au plus n-2 fois (si j'ai bien compris)

Le contraire de "s'annuler au moins n fois", c'est "s'annuler au plus n-2 fois" ? Sûr ?

mais je ne vois pas par ou aller, j'ai essayé d'écrire l'integrale sous forme d'une somme mais ça ne mène nul part

Exploite mon conseil.

[prepsain]

Le contraire de "s'annuler au moins n fois", c'est "s'annuler au plus n-2 fois" ? Sûr ?




Exploite mon conseil.

Ouai mais franchement ça ne m’inspire pas du tout..........Bref, je ne cmprends pas ou il veut aller

[SimonB]

Essaye de répondre à mes questions, déjà. Je ne vais pas te donner la solution toute cuite...

[prepsain]

Essaye de répondre à mes questions, déjà. Je ne vais pas te donner la solution toute cuite...

Au plus n fois désolé! le problème est que en traçant f on est tenté de dire que les aires se compensent (donc f change de signe au moins n fois) mais je fais aussi un graphique ou f s'annule n fois sans qu'elle ne change de signe, les aires ne se compensent plus donc pourquoi l’intégrale vaudrait 0

Au dela du fait que je n'arrive pas à le démontrer, je n'arrive pas non plus à le visualiser :hum:

[Maxmau]

Bonjour,

Je coince un peu sur cet exo:

soit de non identiquement nulle telle que

Montrer que s'annule au moins fois sur

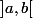
j'ai essayé de raisonner par l'absurde mais ..

Suppose que f s'annule 3 fois en c,d,e. Avec cht de signe a chaque fojs,
Que peut tu dire du produit. (t-c)(t-d)(t-e)f(t) ?

[prepsain]

Suppose que f s'annule 3 fois en c,d,e. Avec cht de signe a chaque fojs,
Que peut tu dire du produit. (t-c)(t-d)(t-e)f(t) ?

Il s'annule aussi trois fois en changeant de signe mais je ne vois pas ou tu veux en venir

[Maxmau]

Il s'annule aussi trois fois en changeant de signe mais je ne vois pas ou tu veux en venir

Ce produjt est de signe constant

[prepsain]

Ce produjt est de signe constant

D'une part je ne vois pas pourquoi ce produit est de signe constant (à moins que je ne sache plus faire un tableau de signe), de plus je ne vois pas le rapport avec mon exo et pour finir (j'en ai un peu marre de cet exos, je suis sur un autre) mon précédent poste disais (le problème est que en traçant f on est tenté de dire que les aires se compensent (donc f change de signe au moins n fois) mais je fais aussi un graphique ou f s'annule n fois sans qu'elle ne change de signe, les aires ne se compensent plus donc pourquoi l’intégrale vaudrait 0 )

:hum:

[SimonB]

On parle des zéros avec changement de signe, pas juste des zéros.
Je ne vois pas de quelles aires qui se compenseraient tu parles, sinon.

[prepsain]

On parle des zéros avec changement de signe, pas juste des zéros.
Je ne vois pas de quelles aires qui se compenseraient tu parles, sinon.

Pour moi pour que s'annule, il faut que les aires sous la courbe se compensent, cela implique que f s'annule n fois en changeant de signe, sauf que lui ne suggère pas que f s'annule en changeant de signe mais simplement s'annule au moins n fois donc je ne vois pas en quoi f s'annulerait n fois.

Pour résumer, je ne comprends pas ce qui se passe concrètement et je n'arrive pas à démontrer par l'absurde que c'est le cas

[Maxmau]

Bonjour,

Je coince un peu sur cet exo:

soit de non identiquement nulle telle que

Montrer que s'annule au moins fois sur

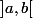
j'ai essayé de raisonner par l'absurde mais ..

Re

Supposons que f s'annule moins de n fois sur ]a,b[
Donc f s'annule k fois avec changement de signe, avec k < n, en les points: a1,a2,......,ak.
Posons: Q(t) = (t - a1)(t - a2).........(t - ak)
Q(t)f(t) est de signe constant sur [a,b]
L'intégrale sur [a,b] est nulle puisque degQ < n
conclusion: Q(t)f(t) est identiquement nul sur [a,b]. f est donc identiquement nulle sur [a,b].
Contradiction