Bonjour voici un exercice d'olympiade : trouver tous les couples (p,q) de nombre premiers vérifiant P^3-q^5=(p+q)^2
Bonne chance.
Cordialement.
Raptor.
Les couples (p,q)
12 messages
- Page 1 sur 1
si
si p et q sont different
q divise p-1 (1)
et p divise
et on a
alors dans tt les cas p divise
=> si p est different de 3
(p divise q+1 ou bien p divise
=>si p divise
=> si p=3
alors
et il ne me rest que le cas ou
p diviseet p ne divise pas
et q divise
je terminerai apres ,je vais sortir maintenant, :++:
salut aviateurpilote,
si un nombre premier p divise q1*q2*...qn,alors p divise q1 ou q2 ou ..qn.donc pas la peine de faire ces étapes :happy2:
tu voulais dire p=kq+1
Cordialement,Amine
aviateurpilot a écrit:et p divise
et on a(3 ou 1)
alors dans tt les cas p diviseou bien p divise
=> si p est different de 3
(p divise q+1 ou bien p divise)
si un nombre premier p divise q1*q2*...qn,alors p divise q1 ou q2 ou ..qn.donc pas la peine de faire ces étapes :happy2:
=>si p divise q^2-q+1
d'apres (1) q=kp+1 (k de N)
tu voulais dire p=kq+1
Cordialement,Amine
merci j'ai pas vu, c pour cela que j'ai pas trouvé la solution
oui je sais
c facile de trouver p divise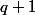 ou
ou 
ou il se peut que p divise les 2 en meme temps
mais moi j'ai fait ces etapes
pour trouver que p divise) ou bien
ou bien )
c-à-dire que p ne peus pas diviser) et
et ) en meme temps , :++:
en meme temps , :++:
amin a écrit:si un nombre premier p divise q1*q2*...qn,alors p divise q1 ou q2 ou ..qn.donc pas la peine de faire ces étapes
oui je sais
c facile de trouver p divise
ou il se peut que p divise les 2 en meme temps
mais moi j'ai fait ces etapes
pour trouver que p divise
c-à-dire que p ne peus pas diviser
aviateurpilot a écrit:2 ou 4 mod 6 =pair
3 mod 6 =multiple de 3
donc tt les nombre premier sauf 3 et 2 sont congru à 1 ou -1 mod 6
et apres
altusi a écrit:tu vérifie tous les cas pour p et q1,-1) (1,1) (-1,-1) (-1,1) et tu remarque que l'égalité ne peut avoir lieu hormis pour quelque petites valeurs
tu as fait une faute là
tu voulais dire que p ou q est egal à {3 ou 2}
car il se peut que p ou q soit >3
donc les couples possibles sont
aviateurpilot a écrit:et il ne me rest que le cas ou
p diviseet q divise
on verifie :
donc S={(7;3)} :zen:
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
