DM sur la droite d'Euler
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 19 Avr 2012, 23:40
par maths0 » 19 Avr 2012, 23:40
Voyons si tu as compris:

Réduire la somme vectorielle suivante en un vecteur:

-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 19 Avr 2012, 23:45
par chomen » 19 Avr 2012, 23:45
Cela fera simplement
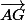
je crois...
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 19 Avr 2012, 23:45
par maths0 » 19 Avr 2012, 23:45
Oui très bien !
Revenons à nos moutons:
D'après l'énoncé:
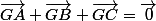
.
Or d'après la relation de Chasles:
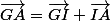
.
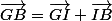
.
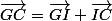
.
On obtient donc:
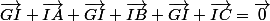
.
En regroupant:
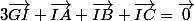
.
Sachant que I est le milieu de [BC]:
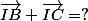
.
B-----I-----C :ptdr:
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 19 Avr 2012, 23:49
par chomen » 19 Avr 2012, 23:49
Je trouve
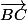
mais je crois que c'est faux...
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 19 Avr 2012, 23:52
par maths0 » 19 Avr 2012, 23:52
Si I est le milieu du segment [BC]:
B----------I----------C

c'est BC
Donc:
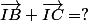
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 19 Avr 2012, 23:54
par chomen » 19 Avr 2012, 23:54
Ah non, ça doit surement être

-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 00:01
par maths0 » 20 Avr 2012, 00:01
Oui ! ouf !

et

Un vecteur existe en tout point du plan:

On reviens sur le point de départ donc c'est vecteur nul.
En regroupant:
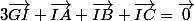
.
Sachant que I est le milieu de [BC]:

.
On retombe sur:
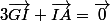
.
Or on veut démontrer que: 
Encore un tour de Chasles .... mais cette fois avec A dans
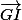
Sachant que logiquement

...
On cherche à retomber sur 
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 20 Avr 2012, 00:06
par chomen » 20 Avr 2012, 00:06
Cela devrait faire

-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 00:10
par maths0 » 20 Avr 2012, 00:10
???
On retombe sur:
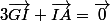
.
or d'après Chasles:

.
Donc:
 + \vec {IA} =\vec 0)
.
Donc:
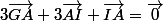
.
On regroupe les AI ..., je rappelle que:
on cherche à retomber sur 
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 00:16
par maths0 » 20 Avr 2012, 00:16
D'après l'énoncé:
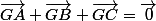
.
Or d'après la relation de Chasles:
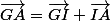
.
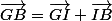
.
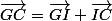
.
On obtient donc:
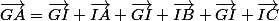
.
En regroupant:
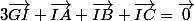
.
Sachant que I est le milieu de [BC]:

.
On retombe sur:
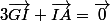
.
Or d'après la relation de Chasles:

.
D'où en remplacant:
 + \vec {IA} =\vec 0)
.
Donc:
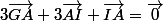
.
Et:

.
En poursuivant:
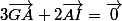
.
En passant de l'autre coté:
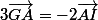
.
Et:
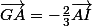
.
Finalement:
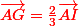
. CQFD
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 20 Avr 2012, 00:18
par chomen » 20 Avr 2012, 00:18
Ah oui merci beaucoup, je m'étais trompé...
Cela va donc faire :

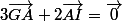
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 00:21
par maths0 » 20 Avr 2012, 00:21
On dit souvent par abus de langage, G se trouve au 2/3 de la médiane (AI).
Ou au 2/3 de [AI].
Ce qui prouve que G est centre de gravité du triangle ABC.
Abus de langage car la médiane est par définition une droite n'a pas de "2/3".
Voilà pour la première question :mur:
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 20 Avr 2012, 00:23
par chomen » 20 Avr 2012, 00:23
D'accord, merci beaucoup de ton aide !
Pourrons nous poursuivre cela plus tard a moins que ça ne te dérange ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 00:24
par maths0 » 20 Avr 2012, 00:24
Non peu importe, bon courage pour la suite.
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 20 Avr 2012, 00:26
par chomen » 20 Avr 2012, 00:26
Merci beaucoup
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 20 Avr 2012, 13:00
par chomen » 20 Avr 2012, 13:00
Cela suffit donc pour justifier que G est le centre de gravité du triangle ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 14:10
par maths0 » 20 Avr 2012, 14:10
Oui cela suffit. Avec la relation vectorielle de AG en fonction de AI tu peux placer G.
Donc savoir où il est (2/3 de la médiane). Et donc savoir que c'est le centre de gravité.
Alors qu'avec GA+GB+GC=0 si je te demande placer G tu ne "peux pas".
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 20 Avr 2012, 14:13
par chomen » 20 Avr 2012, 14:13
Et pour la suite, je pense avoir une idée :
Pour démontrer que O,H et G sont alignée, on démontre que

sont colinéaires à l'aide des calculs précédents...
Est-ce bien ça ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 14:14
par maths0 » 20 Avr 2012, 14:14
Il y a de l'idée ...
Dans quel cas 2 vecteurs sont colinéaires ?
-
chomen
- Membre Naturel
- Messages: 35
- Enregistré le: 19 Avr 2012, 19:33
-
 par chomen » 20 Avr 2012, 14:18
par chomen » 20 Avr 2012, 14:18
Lorsque par exemple on a k
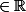
et donc que
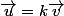
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités

