Calcul avec ln et exp
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Mulan
- Membre Relatif
- Messages: 131
- Enregistré le: 11 Oct 2011, 19:03
-
 par Mulan » 14 Avr 2012, 12:20
par Mulan » 14 Avr 2012, 12:20
Bonjour,
J'ai juste besoin de votre aide pour montrer que
ln( ( 1+ exp(2x) / 1 +exp(-2x) ) = 2x
Je bloque dessus j'ai essayé de résoudre ( 1+ exp(2x) / 1 +exp(-2x) ) en multipliant en haut et en bas par le denominateur mais je n'aboutit à rien.
Merci
-
gdlrdc
- Membre Relatif
- Messages: 160
- Enregistré le: 24 Jan 2009, 18:11
-
 par gdlrdc » 14 Avr 2012, 12:42
par gdlrdc » 14 Avr 2012, 12:42
Tu aimerais montrer que ( 1+ exp(2x) / 1 +exp(-2x) ) = exp(2x).
ce qui reviens à montrer quoi en multipliant chaque membre de l'égalité par exp(-2x) ?
-
Mulan
- Membre Relatif
- Messages: 131
- Enregistré le: 11 Oct 2011, 19:03
-
 par Mulan » 14 Avr 2012, 12:57
par Mulan » 14 Avr 2012, 12:57
gdlrdc a écrit:Tu aimerais montrer que ( 1+ exp(2x) / 1 +exp(-2x) ) = exp(2x).
ce qui reviens à montrer quoi en multipliant chaque membre de l'égalité par exp(-2x) ?
En multipliant par exp(-2x), on obtient :
ln ( exp(-2x) + 1 / exp(-2x) + exp(-4x) ) et la je ne sais pas quoi faire non plus
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 14 Avr 2012, 15:20
par Elerinna » 14 Avr 2012, 15:20
Mulan a écrit:ln( ( 1+ exp(2x) / 1 +exp(-2x) ) = 2x
Gare aux parenthèses faisant défaut. La composée
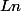
porte soit sur :

soit sur la fraction globale. Dans les deux cas, la réciproque du logarithme népérien est
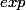
et on a par application de la propriété

la relation :
=x)
.
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 14 Avr 2012, 15:53
par antonyme » 14 Avr 2012, 15:53
Elerinna a écrit: Mulan a écrit:ln( ( 1+ exp(2x) / 1 +exp(-2x) ) = 2x
Gare aux parenthèses faisant défaut.
En faite là il y a surtout une parenthèse ouverte en trop. Mais ln porte bien sur la fraction globale.
-
Mulan
- Membre Relatif
- Messages: 131
- Enregistré le: 11 Oct 2011, 19:03
-
 par Mulan » 14 Avr 2012, 16:03
par Mulan » 14 Avr 2012, 16:03
antonyme a écrit:En faite là il y a surtout une parenthèse ouverte en trop. Mais ln porte bien sur la fraction globale.
le ln porte sur la fraction mais je suis quand même bloquer
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 14 Avr 2012, 16:16
par geegee » 14 Avr 2012, 16:16
Mulan a écrit:Bonjour,
J'ai juste besoin de votre aide pour montrer que
ln( ( 1+ exp(2x) / 1 +exp(-2x) ) = 2x
Je bloque dessus j'ai essayé de résoudre ( 1+ exp(2x) / 1 +exp(-2x) ) en multipliant en haut et en bas par le denominateur mais je n'aboutit à rien.
Merci
Bonjour,
ln( ( 1+ exp(2x) / 1 +exp(-2x) ) =ln(((exp(2x)+exp(4x))/(exp(2x)+1))=ln(((X+X^2)/(X+1))=ln(X)+ln(1+X) -ln(X+1)=ln(e^2x)= 2x
ln(a/b)=ln(a)-ln(b)
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 14 Avr 2012, 16:24
par antonyme » 14 Avr 2012, 16:24
Mulan a écrit: gdlrdc a écrit:Tu aimerais montrer que ( 1+ exp(2x) / 1 +exp(-2x) ) = exp(2x).
ce qui reviens à montrer quoi en multipliant chaque membre de l'égalité par exp(-2x) ?
En multipliant par exp(-2x), on obtient :
ln ( exp(-2x) + 1 / exp(-2x) + exp(-4x) ) et la je ne sais pas quoi faire non plus
Si tu suis le conseil de gdlrdc tu obtient :

To be continued...
-
Mulan
- Membre Relatif
- Messages: 131
- Enregistré le: 11 Oct 2011, 19:03
-
 par Mulan » 14 Avr 2012, 16:26
par Mulan » 14 Avr 2012, 16:26
antonyme a écrit:Si tu suis le conseil de gdlrdc tu obtient :

To be continued...
justement mon probleme est que je tombe sur :
( exp(-2x) + 1 / exp(-2x) + exp(-4x) ) = 1
et la je ne sais pas quoi faire
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 14 Avr 2012, 16:41
par antonyme » 14 Avr 2012, 16:41
Mulan a écrit:justement mon probleme est que je tombe sur :
( exp(-2x) + 1 / exp(-2x) + exp(-4x) ) = 1
et la je ne sais pas quoi faire
Il ne faut pas multiplier le dénominateur :langue:
-
Mulan
- Membre Relatif
- Messages: 131
- Enregistré le: 11 Oct 2011, 19:03
-
 par Mulan » 14 Avr 2012, 17:28
par Mulan » 14 Avr 2012, 17:28
antonyme a écrit:Il ne faut pas multiplier le dénominateur :langue:
Ah oui je suis allez trop vite
Du coup j'ai du
(exp(-2x) + 1) / (1 + exp(-2x)) = 1
C'est un peu bizarre ca me donne 1 = 1 du coup y a pas d'interet ?
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 14 Avr 2012, 17:38
par antonyme » 14 Avr 2012, 17:38
Mulan a écrit:Ah oui je suis allez trop vite
Du coup j'ai du
(exp(-2x) + 1) / (1 + exp(-2x)) = 1
C'est un peu bizarre ca me donne 1 = 1 du coup y a pas d'interet ?
Mais c'est exactement ce que tu voulais montré mais on l'a fais dans le désordre.
Il faut que tu reparte de :
ln( 1+ exp(2x) / 1 +exp(-2x) ) = ln( exp(2x) * ( exp(-2x) + 1 / 1 +exp(-2x) ) ) = ln( exp(2x) ) = 2x
:zen:
-
Mulan
- Membre Relatif
- Messages: 131
- Enregistré le: 11 Oct 2011, 19:03
-
 par Mulan » 14 Avr 2012, 17:42
par Mulan » 14 Avr 2012, 17:42
antonyme a écrit:Mais c'est exactement ce que tu voulais montré mais on l'a fais dans le désordre.
Il faut que tu reparte de :
ln( 1+ exp(2x) / 1 +exp(-2x) ) = ln( exp(2x) * ( exp(-2x) + 1 / 1 +exp(-2x) ) ) = ln( exp(2x) ) = 2x
:zen:
Euh non, il y a quelque chose qui me bloque en montrant que :
exp(2x) * ( exp(-2x) + 1 / 1 +exp(-2x) ) = 1
comment pouvez vous trouver ln(exp(2x)) car ln(1) = 0
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 14 Avr 2012, 17:50
par antonyme » 14 Avr 2012, 17:50
Mulan a écrit:Euh non, il y a quelque chose qui me bloque en montrant que :
exp(2x) * ( exp(-2x) + 1 / 1 +exp(-2x) ) = 1
comment pouvez vous trouver ln(exp(2x)) car ln(1) = 0
( exp(-2x) + 1 / 1 +exp(-2x) ) =
1exp(2x) *
( exp(-2x) + 1 / 1 +exp(-2x) ) =
exp(2x) *
1 :zen:
En LaTeX :
 = ln( e^{2x} \times \frac{e^{-2x} + 1}{1 +e^{-2x}} ) = ln( e^{2x} ) = 2x)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
