Espace de Sobolev
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Jan 2012, 14:25
par izoard » 09 Jan 2012, 14:25
Bonjour, j'ai une question à propos des espaces de Sobolev définis sur des espaces non bornés,
ici sur

Lorsque je regarde une fonction u de
)
je pense que j'ai toujours u(0)=0 mais par contre je ne sais pas si
 =0)
Si quelqu'un connait une démo ...
J'ai essayé de le faire à partir de la densité de
 \ dans \ H^1_0 (I))
mais je n'ai pas abouti
Merci d'avance
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 09 Jan 2012, 21:15
par girdav » 09 Jan 2012, 21:15
Qu'est-ce que tu entends par "tend vers 0 en l'infini". Les fonctions de
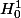
ne sont définies qu'à l'égalité presque partout près.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Jan 2012, 21:18
par izoard » 09 Jan 2012, 21:18
Je considère le representant continu de la classe d'une fonction de

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 09 Jan 2012, 22:13
par girdav » 09 Jan 2012, 22:13
Le résultat est vrai; la clé est que
)
s'injecte dans
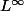
.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Jan 2012, 22:16
par izoard » 09 Jan 2012, 22:16
Mon problème est que en fait je ne vois même pas quelle est la definition de
)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 09 Jan 2012, 23:13
par girdav » 09 Jan 2012, 23:13
izoard a écrit:Mon problème est que en fait je ne vois même pas quelle est la definition de
)
C'est l'adhérence de l'espace des fonctions test pour la norme de
)
: il est donc inclus dans
)
, et on montre que le fait que
\to 0)
quand

tend vers l'infini est vrai pour les fonctions de
)
.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 10 Jan 2012, 10:05
par izoard » 10 Jan 2012, 10:05
J'ai trouvé la démo dans le brézis ! Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités