Continuité fonction

[zork]

bonjour,

si y non nul, 0 si y=0

montrer que f est continue

le problème est en y=0


j'arrive à f(x,y)<=|x| mais comment continuer ensuite

merci

[Nightmare]

Salut,

tu as effectivement que pour tout x et y,

mais que vaut ?

[zork]

mais là c'est quelque soit x donc je ne peut pas faire tendre x vers 0.
d'autre part si je reprend la définition que j'ai écrite, comment je ferai?

[Nightmare]

Je ne comprends pas, qu'entends-tu par "c'est quel que soit x" ?

On cherche bien à montrer la continuité en (0,0) non?

[barbu23]

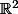
On cherche à montrer la continuité sur tout entier. :happy3:

[Nightmare]

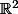
On cherche à montrer la continuité sur tout entier. :happy3:

Ailleurs qu'en (0,0) la continuité est immédiate.

[barbu23]

Ah oui, c'est vrai. :happy3:

[zork]

ce n'est pas en (0,0)
c'est en (x,0) il y a indétermination que lorsque y=0

[zork]

comment trouver le domaine de différentiabilité de f
j'ai du mal avec g(x,y)=xsin(1/y)
je veux montrer qu'elle n'est pas différentiable en (x,0)
j'utilise la définition avec la limite qui doit tendre vers 0 et comme le sinus n'a pas de limite
je trouve que l'ensemble de différentiabilité de f est R\{(x,0)}xR

d'autre part pour les dérivées partielles en particulier pour g(x,y)=xsin(1/y)
comment montrer qu'elle est ou n'est pas dérivable en (x,0)?

en faites dans cet exo mon problème vient de la définition de f: on a juste y=0 alors que d'habitude c'est (x,y)=0

[zork]

personne ne peut m'expliquer quel est la différence
si y=0 au lieu de (x,y)=0

[fal]

si y non nul, 0 si y=0

montrer que f est continue

le problème est en y=0
[TEX]|(0,y)|0
alors poour tout y non nul f(x,y)<= absolu(x) qui tend vers 0 quand x tend vers 0 independamment de y
donc f(x,y) tend vers 0 en (0,0), or f(0,0)=0

[zork]

ok c'est bon merci