Espace de sobolev

[izoard]

Bonjour,
soit u une fonction H1 de Rd dans R .

on sait par hypothese que grad(u)=0

J' imagine que cela veut dire que grad(u)=0 presque partout .

Je n'arrive pas à voir pourquoi on aurait alors u=cst presque partout .

Plus précisement, je ne comprend pas pourquoi c'est la même constante sur Rd tout entier

Merci

[girdav]

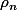
On prend une suite régularisante ; à la sous-suite près, converges presque partout vers , et est une fonction de gradient nul. On se sert de la connexité de pour voir que presque partout, où est une constante.

[izoard]

Ok, j'ai bien compris la démo à part un point : comment montrer que le gradient du produit de convolution est nul ???

En effet, d'habitude, quand on dérive un produit de convolution, on dérive la suite régularisante non ?!

[girdav]

Ça marche aussi pour les dérivées faibles. Il faut l'écrire, c'est une conséquence de Fubini, et c'est le point central de la preuve. Je te donnerai les détails si tu n'y parviens pas.

[izoard]

Je note tn ma suite régularisante .

En fait on aurait donc (tn*u)'=tn*(u') ??

Dans quel livre pourrais-je trouver un peu plus plus de précision sur le lien entre la convolution et les dérivées faibles ??

PS : merci pour la réponse, je ne l'avais jamais trouvée rédigée proprement

[izoard]

J'ai une question dans un tout autre domaine . Peut être as ru la réponse car tu à l'air costaud en analyse :lol3:

je travaille sur l'equation de burgers avec comme condition initiale u0(x)=sin(x)
Il apparait un choc au temps t=1 .
Je n'arrive pas à determiner à l'aide des conditions de Rankine Hugoniot la vitesse de propagation de la discontinuité .

[girdav]

Si tu as une autre question, il vaut mieux ouvrir un autre topic. D'ailleurs, n'étant pas particulièrement expert en EDP, il faudra que tu donnes un peu plus de contexte, ou quelques définitions, ou au moins un lien vers celles-ci.