Comment étudier cette suite ?

[Skullkid]

Pour la n-ième fois, tu n'as pas à choisir u0 ! Il est fixé, il est unique, tu connais certaines de ses propriétés, mais tu ne le choisis pas.

Bon, tu as montré que . Je ne répondrai pas à tes questions "on doit faire ça ?" et "on doit dire ça ?". Tu es une grande personne, tu n'as pas besoin de ma permission pour essayer un truc. Donc essaye un truc, poste le résultat de tes essais, et là on pourra avancer.

[Dante0]

Pour la n-ième fois, tu n'as pas à choisir u0 ! Il est fixé, il est unique, tu connais certaines de ses propriétés, mais tu ne le choisis pas.

Bon, tu as montré que . Je ne répondrai pas à tes questions "on doit faire ça ?" et "on doit dire ça ?". Tu es une grande personne, tu n'as pas besoin de ma permission pour essayer un truc. Donc essaye un truc, poste le résultat de tes essais, et là on pourra avancer.

Mais c'est ce qu'a fait mon prof ! Il a choisi
Je ne sais pas comment montrer qu'elle est bornée avec uniquement la lettre et pas la valeur numérique (ne me dit pas : "tu viens de le faire !!" ... )

Et puis d'ailleurs si je ne connais pas la valeur numérique de comment suis-je censé trouver le signe de ?

[Skullkid]

Mais c'est ce qu'a fait mon prof ! Il a choisi

Sans doute pour montrer un exemple de telle suite, mais il n'a sûrement pas fait une démonstration avec ça.

Je ne sais pas comment montrer qu'elle est bornée avec uniquement la lettre et pas la valeur numérique

Pourtant la définition de "bornée" ne contient que des lettres et aucune valeur numérique, à ma connaissance. C'est quoi comme type de suite, la suite ?

Et puis d'ailleurs si je ne connais pas la valeur numérique de comment suis-je censé trouver le signe de ?

Tu ne peux pas le trouver, mais un nombre réel ça peut être soit strictement positif, soit strictement négatif, soit nul. 3 possibilités, pas une de plus. Si jamais u1 - u0 est strictement positif, qu'est-ce qui se passe ? Si jamais u1 - u0 est strictement négatif, qu'est-ce qui se passe ? Si jamais u1 - u0 est nul, qu'est-ce qui se passe ?

[Dante0]

Sans doute pour montrer un exemple de telle suite, mais il n'a sûrement pas fait une démonstration avec ça.



Pourtant la définition de "bornée" ne contient que des lettres et aucune valeur numérique, à ma connaissance. C'est quoi comme type de suite, la suite ?

Une suite définie par une relation de récurrence...
Dans cet exercice il faut réciter les définitions en fait (qui contiennent des lettres) ou bien répondre aux questions ?


Tu ne peux pas le trouver, mais un nombre réel ça peut être soit strictement positif, soit strictement négatif, soit nul. 3 possibilités, pas une de plus. Si jamais u1 - u0 est strictement positif, qu'est-ce qui se passe ? Si jamais u1 - u0 est strictement négatif, qu'est-ce qui se passe ? Si jamais u1 - u0 est nul, qu'est-ce qui se passe ?

Ok , donc il faut distinguer les cas ... Je pensais donner une réponse directe ...

[Skullkid]

Oui, il faut distinguer les cas si tu veux te retrouver dans une situation où tu connais le signe de u1-u0. Maintenant, as-tu vraiment besoin de connaître le signe de u1-u0 ?

Pour ce qui est de la suite u(n+1)-un, tu as montré une relation plus tôt, ça devrait te dire quelque chose.

[Dante0]

Oui, il faut distinguer les cas si tu veux te retrouver dans une situation où tu connais le signe de u1-u0. Maintenant, as-tu vraiment besoin de connaître le signe de u1-u0 ?

Pour ce qui est de la suite u(n+1)-un, tu as montré une relation plus tôt, ça devrait te dire quelque chose.

Ah bah oui , j'ai montré qu'elle était croissante en utilisant la dérivée ... Mais est-ce que j'ai le droit de le faire ?

Sinon il n'y a qu'a dire :
si la suite est monotone (croissante)
si la suite est décroissante
si la suite est constante

Mais le problème c'est que je ne sais pas si est plus grand ou non que ... (en admettant que ma technique avec la dérivée ne soit pas la bonne technique à utiliser).

[Skullkid]

Ah bah oui , j'ai montré qu'elle était croissante en utilisant la dérivée ... Mais est-ce que j'ai le droit de le faire ?

Tu as montré que qui était croissante ? En utilisant la dérivée de qui ?

[Anonyme]

@Dante0
Ceci est juste un message à titre de complément d'information
Es tu d'accord sur ce qui est écrit dans ce message ?

C'est juste pour vérifier si tu ne confonds pas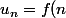 les suites du type avec les suites du type

Ma question est : es tu ok avec ce qui est écrit ci-dessous dans 1) et 2) ?

Soit une suite récurrente définie par (avec aucun problème de définition) et avec une fonction dérivable ,

1) si la fonction est croissante alors la suite 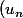est monotone et son "type de monotonie" dépend du signe de

2) si la fonction est décroissante on ne peut rien conclure sur cette suite et en général on étudie les suites extraites et

si oui alors désolé de t'avoir embêté avec ce message
si non alors il faut que tu relises ton cours sur les suites du type

Dans ton exercice on a :
la suite qui est définie par un 1ier terme tel que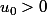
et par la relation de récurrence avec
soit strictement décroissante si

Remarque :
Dans cet exercice , tu peux aussi également étudier la suite définie par 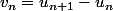car c'est une suite géométrique...
Mais à mon avis, c'est "mieux" de comprendre le "raisonnement général" expliqué ci dessus.

[Dante0]

Tu as montré que qui était croissante ? En utilisant la dérivée de qui ?

Car à priori la dérivée de f est positive. Puisque
Donc elle est croissante , ce qui signifie que tous les termes de la suites sont positifs puisque

Elle est donc monotone.

La dérivée de en posant

@Dante0
Ceci est juste un message à titre de complément d'information
Es tu d'accord sur ce qui est écrit dans ce message ?

C'est juste pour vérifier si tu ne confonds pas les suites du type avec les suites du type

Ma question est : es tu ok avec ce qui est écrit ci-dessous dans 1) et 2) ?

Soit une suite récurrente définie par (avec aucun problème de définition) et avec une fonction dérivable ,

1) si la fonction est croissante alors la suite est monotone et son "type de monotonie" dépend du signe de

2) si la fonction est décroissante on ne peut rien conclure sur cette suite et en général on étudie les suites extraites et

si oui alors désolé de t'avoir embêté avec ce message
si non alors il faut que tu relises ton cours sur les suites du type

Dans ton exercice on a :
la suite qui est définie par un 1ier terme tel que
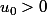
et par la relation de récurrence avec
soit strictement décroissante si

Remarque :
Dans cet exercice , tu peux aussi également étudier la suite définie par car c'est une suite géométrique...
Mais à mon avis, c'est "mieux" de comprendre le "raisonnement général" expliqué ci dessus.

Oui ... Je suis d'accord avec ce que tu dis ... Sauf que je vois pas ce que viennent faire les suites extraites ici (jamais fait ca)
Donc du coup elle est croissante (cf ma citation au dessus) ?

[Anonyme]

Oui ... Je suis d'accord avec ce que tu dis ... Sauf que je vois pas ce que viennent faire les suites extraites ici (jamais fait ca)
Donc du coup elle est croissante (cf ma citation au dessus) ?

Bonjour
Si ton message veut dire que le fonction est croissante , c'est correct.
Si ton message veut dire que la suite est croissante c'est faux

ps)
Explications sur les 2 suites extraites dans le cas d'une fonction décroissante.
Si la fonction est décroissante alors la fonction est croissante
C'est pour cela qu'on étudie en général les 2 suites extraites et
On a
, , .... etc...
, , .... etc...

et la suite converge si et seulement si ces 2 suites extraites convergent vers la même limite L

[Dante0]

Bonjour
Si ton message veut dire que le fonction est croissante , c'est correct.
Si ton message veut dire que la suite est croissante c'est faux

ps)
Explications sur les 2 suites extraites dans le cas d'une fonction décroissante.
Si la fonction est décroissante alors la fonction est croissante
C'est pour cela qu'on étudie en général les 2 suites extraites et
On a
, , .... etc...
, , .... etc...

et la suite converge si et seulement si ces 2 suites extraites convergent vers la même limite L

Voila , c'est de la que vient ma confusion.
Vous allez surement me dire d'aller voir mon cours , et je vous dirais que me je souviens très bien avoir vu dans mon cours : soit , si f est croissante alors la suite u_n est croissante , l'inverse n'est pas vrai. La fonction influence la suite , mais la suite n'influence pas la fonction.

Je ne comprends pas ton explication sur les suites extraites , mais inutile de les évoquer ici je pense , je verrais ca une autre fois (on va éviter de faire un topic à 10pages).

[Anonyme]

Voila , c'est de la que vient ma confusion.
Vous allez surement me dire d'aller voir mon cours , et je vous dirais que me je souviens très bien avoir vu dans mon cours : soit , si f est croissante alors la suite u_n est croissante , l'inverse n'est pas vrai. La fonction influence la suite , mais la suite n'influence pas la fonction.

Je ne comprends pas ton explication sur les suites extraites , mais inutile de les évoquer ici je pense , je verrais ca une autre fois (on va éviter de faire un topic à 10pages).

Regarde de nouveau plus attentivement ton cours , car tu as certainement mal interprété les explications.

Dans cet exercice si alors la suite est décroissante

[Dante0]

Regarde de nouveau plus attentivement ton cours , car tu as certainement mal interprété les explications.

Dans cet exercice si alors la suite est décroissante

Ok ... Mais comment le savoir ? :mur:
Comment savoir si u1 est plus grand que u0 (parce la je comprends pas du tout les explications de SkullKid à ce sujet)

[Anonyme]

Ok ... Mais comment le savoir ? :mur:
Comment savoir si u1 est plus grand que u0 (parce la je comprends pas du tout les explications de SkullKid à ce sujet)

Il suffit de comparer et
et donc il y a étudier 3 cas (et vérifier qu'il sont compatibles avec les conditions de ton énoncé c'est à dire et
3ième cas :

L'énoncé de cet exercice n'impose pas de prendre un donné.

[Dante0]

[quote="schulhof"]Il suffit de comparer et
et donc il y a étudier 3 cas (et vérifier qu'il sont compatibles avec les conditions de ton énoncé c'est à dire et
3ième cas : ?

[Anonyme]

Ok , donc je pose ?

Il faut étudier les 3 cas et calculer les conditions de ces 3 cas sur

Je ne comprends pas ton problème.

Par exemple le 1ier cas est : peut on avoir et si oui pour quelle valeur de ?
On doit donc chercher à résoudre
C'est une équation du 1ier degré à 1 inconnue qui est donc théoriquement facile à résoudre...

Si tu as un problème de compréhension remplace par , cela t'aidera peut être ?
Dans cette équation est un nombre donné.

[Dante0]

Il faut étudier les 3 cas et calculer les conditions de ces 3 cas sur

Je ne comprends pas ton problème.

Par exemple le 1ier cas est : peut on avoir et si oui pour quelle valeur de ?
On doit donc chercher à résoudre
C'est une équation du 1ier degré à 1 inconnue qui est donc théoriquement facile à résoudre...

Si tu as un problème de compréhension remplace par , cela t'aidera peut être ?
Dans cette équation est un nombre donné.

En calculant , ce que j'ai fait dans mon message précédent on peut conclure que non ?

[Anonyme]

En calculant , ce que j'ai fait dans mon message précédent on peut conclure que non ?

Non la résolution de l'équation n'est pas correcte
Regarde bien attentivement ce que tu as écrit (remplace par la variable , si cela t'aide et par le nombre )

Question :
Es tu en classe de terminale S ?
et est ce que votre prof de maths vous a expliqué comment on fait "graphiquement" :
représentation graphique des 1iers termes d'une telle suite ?

c'est à dire dessiner le graphe de la fonction f , et dessiner sur l'axe des abscisses u_0 , u_1 , u_2 ....etc... avec l'aide de la droite d'équation y=x

[Dante0]

Non la résolution de l'équation n'est pas correcte
Regarde bien attentivement ce que tu as écrit (remplace par la variable , si cela t'aide et par le nombre )

Question :
Es tu en classe de terminale S ?
et est ce que votre prof de maths vous a expliqué comment on fait "graphiquement" :
représentation graphique des 1iers termes d'une telle suite ?

c'est à dire dessiner le graphe de la fonction f , et dessiner sur l'axe des abscisses u_0 , u_1 , u_2 ....etc... avec l'aide de la droite d'équation y=x

J'etais en ES...




Je vois pas ce qui est faux... :hein:

[Anonyme]

J'etais en ES...




Je vois pas ce qui est faux... :hein:

Résoudre une équation du 1ier degré à 1 seule inconnue revient à trouver la valeur de l'inconnue.

Dans cette équation il faut finir par pouvoir écrire

Visiblement tu as beaucoup de difficultés avec "le calcul littéral" / les équations avec des paramètres

Je te conseille de remplacer le nombre par un "VRAI nombre"
de prendre par exemple :
et d'essayer de résoudre

ps) es tu toujours en terminale ES ?