Etude de fonction ln
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
wako
- Messages: 7
- Enregistré le: 18 Déc 2010, 12:41
-
 par wako » 18 Déc 2010, 12:47
par wako » 18 Déc 2010, 12:47
Bonjour, je souhaiterai connaitre la méthode pour résoudre ces deux questions :
- soit la fonction f(x)= x [(lnx)² + 1]
- quell est la limite de x(ln x)² pour x -> 0+
- quel est le sens de variation de f(x) sur [0,1]
Merci pour vos réponses !
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 18 Déc 2010, 12:50
par Euler07 » 18 Déc 2010, 12:50
1. 0 tu as lu ton cours ?
2. Dérivation
-
wako
- Messages: 7
- Enregistré le: 18 Déc 2010, 12:41
-
 par wako » 18 Déc 2010, 13:35
par wako » 18 Déc 2010, 13:35
1. euh ... j'ai pas de cours vu que je ne suis pas élève, mais c'est pas grave.
je sais que lim x lnx -> 0 pour x -> 0+ et lim lnx = - infini mais du coup ça fait forme indéterminée ...
2.
f'(x) = ln x ( 2 + ln x ) + 1 et là ? impossible de trouver le signe de ceci ...

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 18 Déc 2010, 13:41
par Olympus » 18 Déc 2010, 13:41
Salut !
En général, pour tous
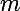
et
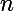
dans

:
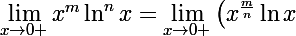^n = \lim_{x \to 0+} \left( \frac{n}{m} x^{\frac{m}{n}} \ln \left(x^{\frac{m}{n}}\right) \right)^n = ...)
^^
-
wako
- Messages: 7
- Enregistré le: 18 Déc 2010, 12:41
-
 par wako » 18 Déc 2010, 14:19
par wako » 18 Déc 2010, 14:19
et soit X=x^m/n du coup X ln X -> 0 . Ok cool merci ! au fait comment tu fais pour écrire avec les signes maths ?
et pour le 2, une idée ?
-
Black Jack
 par Black Jack » 18 Déc 2010, 15:20
par Black Jack » 18 Déc 2010, 15:20
1)
lim(x --> 0+) [x.(ln²(x)+1)] = lim(x --> 0+) [(ln²(x)+1)/(1/x)] est de la forme indéterminée -oo/+oo ---> règle de Lhospital.
= lim(x --> 0+) [(2ln(x)/x)/(-1/x²)] = lim(x --> 0+) [(-2x.ln(x)] = -2.lim(x --> 0+) [ln(x)/(1/x)] est de la forme indéterminée -oo/+oo ---> règle de Lhospital.
= -2.lim(x --> 0+) [(1/x)/(-1/x²)] = -2.lim(x --> 0+) [-x] = 0
********
2)
f '(x) = (ln²(x) + 1) + 2ln(x) = (ln(x) + 1)²
Et ce devrait pas être trop difficile alors de trouver le signe de f '(x) en fonction de x ...
:zen:
-
wako
- Messages: 7
- Enregistré le: 18 Déc 2010, 12:41
-
 par wako » 19 Déc 2010, 01:43
par wako » 19 Déc 2010, 01:43
Merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités