Bonjour
on s'est donné dans un exercice la suite de fonctions définies par
= (1- \frac{x}{n})^n si x < n et f_n (x) = 0)
sinon (on travaille dans R+). On montre facilement que cette suite converge simplement vers la fonction
 = e^{-x})
Pour la convergence uniforme, on montre d'abord que
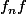
pour tout n , et on divise naturellement R+ en deux intervalles : [0,n] et
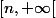
. Pour le premier intervalle, je veux utiliser la méthode suivante :
En posant
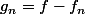
cette fonction étant continue sur cet intervalle, elle atteint son maximum en un point

pour lequel la dérivée est nulle. Tout calcul fait en prenant en compte cette condition nous donne
 = \frac{t_0}{n} e^{-t_0})
.
Seulement pour appliquer cette méthode, je dois être sûr que

soit un maximum local (différent de 0 et n)
Quelqu'un pourrait m'indiquer comment le prouver ??
Merci d'avance
