Une inégalité bien sympa ;)
Olympiades mathématiques, énigmes et défis
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 29 Oct 2010, 17:21
par Malo » 29 Oct 2010, 17:21
Salut !
Voilà une petite inégalité d'OIM sur laquelle je bloque ! :p
Tout d'abord, les présentations : tadam l'inégalité :
Soient x, y et z des réels positifs tels que

Démontrez que :

Bon alors si je réduis tout au même dénominateur, ça devrait marcher non ?
Merci merci !
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 29 Oct 2010, 17:40
par arnaud32 » 29 Oct 2010, 17:40
je te conseille neanmoins
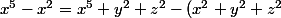)
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 29 Oct 2010, 17:50
par Malo » 29 Oct 2010, 17:50
Oui, merci de l'astuce ! Je reposte quand j'aurais déjà fait ce travail ! :)
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 29 Oct 2010, 18:04
par Malo » 29 Oct 2010, 18:04
J'obtiens :

C'est correct ?
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 29 Oct 2010, 20:30
par Malo » 29 Oct 2010, 20:30
Quelqu'un pourrait-il vérifier ce résultat svp ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 29 Oct 2010, 22:55
par arnaud32 » 29 Oct 2010, 22:55
oui puis tu factorise par x²+y²+z²
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 30 Oct 2010, 10:27
par Malo » 30 Oct 2010, 10:27
Merci

Alors j'ai :
* \frac{1}{x^5-y^5-z^5})
C'est ok ?
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 30 Oct 2010, 11:01
par Rebelle_ » 30 Oct 2010, 11:01
Bonjour =)
J'ai peut que ça ne soit pas bon, quand on développe cette forme on ne retrouve pas celle du début :/
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 30 Oct 2010, 11:19
par Malo » 30 Oct 2010, 11:19
Merci de ta réponse =) Je crois que j'ai mélangé les inverses et les dénominateurs :p
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 30 Oct 2010, 11:25
par Rebelle_ » 30 Oct 2010, 11:25
Je pense aussi ^^'

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Oct 2010, 14:13
par Olympus » 30 Oct 2010, 14:13
Bonjour !
J'ai une solution très élégante si vous êtes intéressés :zen:
On a

, donc il nous suffira de montrer que

, c'est à dire

.
Lemme :
 \in \mathbb{R}_+^*^3 \right) \qquad : \qquad \frac{x^3yz+xy^3z+xyz^3}{x^5+xy^3z+xyz^3} \leq \frac{3\left(y^2+z^2\right)}{2\left(x^2+y^2+z^2 \right)}) Démonstration
Démonstration :
L'inégalité est équivalente à :

Or par AM-GM on a :

En sommant on a notre lemme .
On applique notre lemme, on somme cycliquement, et hop on a l'inégalité recherché


-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Oct 2010, 14:40
par Olympus » 30 Oct 2010, 14:40
Je crois que c'est à déplacer à la section "Olympiades", car sinon, le topic serait vite noyé ici ...
Sinon, de quelle OIM est tirée cette inégalité ?
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 30 Oct 2010, 15:47
par Malo » 30 Oct 2010, 15:47
Salut Olympus !
Trois choses :
- Ta solution est élégante, mais je n'ai pas vu les sommes cycliques encore donc désolé, je comprends pas tout =)
- Bonne idée de déplacer le topic !
- Cet exercice est le 3ème de l'OIM 2005.
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 30 Oct 2010, 15:51
par Rebelle_ » 30 Oct 2010, 15:51
Excusez mon ignorance, OIM veut-il bien dire Olympiades Internationales de Mathématiques (merci Google ^^') ?
Si oui je comprends pourquoi je n'avais pas trop d'idées là-dessus :P
En effet la solution est fort intéressante ! :)
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 30 Oct 2010, 15:52
par Malo » 30 Oct 2010, 15:52
Tout à fait, Rebelle :)
Je revérifie mon histoire de facto et je reposte ;p

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Oct 2010, 15:54
par Olympus » 30 Oct 2010, 15:54
Mon

ci-dessus dit juste "permutez mes variables cycliquement et vous aurez mes deux autres termes", c'est juste une notation car c'est chiant d'écrire les inégalités entièrement avec le LaTeX ^^
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 30 Oct 2010, 15:58
par Malo » 30 Oct 2010, 15:58
Ok. Bah sinon pour la facto, je vois pas dautre solution que de mettre "simplement"
(\frac{1}{x^5+y^2+z^2^}...))
Je vois pas comment simplifier plus ^^
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 30 Oct 2010, 16:02
par Malo » 30 Oct 2010, 16:02
Ouais mais non !
Si l'on étudie l'inégalité avec les x^2, y^2 et z^2 et comme membre de droite 3, on peut appliquer Cauchy Schwarz aux triplets (x^5/2,y,z) et (x^-1/2,y,z)

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Oct 2010, 16:19
par Olympus » 30 Oct 2010, 16:19
Effectivement, ça marche aussi avec Cauchy-Schwarz et l'inégalité triviale

:++:
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 30 Oct 2010, 16:40
par Malo » 30 Oct 2010, 16:40
Olympus a écrit:Effectivement, ça marche aussi avec Cauchy-Schwarz et l'inégalité triviale

:++:
Merci de ton aide

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
