Une inégalité sympa
Olympiades mathématiques, énigmes et défis

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 16 Nov 2009, 21:21
par Olympus » 16 Nov 2009, 21:21
Bonjour,
bon voilà, ce sera la première fois que je vous propose un petit défi ( que j'ai déjà fait, faut bien que je m'entraine vu que les olympiades approchent :ptdr: ) :
Soient

,
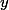
et

trois réels strictement positifs, tel que
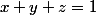
.
Montrer que :
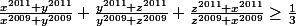
.
Bonne chance !

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 17 Nov 2009, 14:35
par Olympus » 17 Nov 2009, 14:35
Bon bah demain je posterai un indice alors ...

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 18 Nov 2009, 10:31
par Olympus » 18 Nov 2009, 10:31
Bon voici un indice ( peut-être que j'aurais trop dit alors ) :
Montrer que :
 ^2 }{4})
-
Anonyme
 par Anonyme » 18 Nov 2009, 12:51
par Anonyme » 18 Nov 2009, 12:51
Olympus a écrit:Bon voici un indice ( peut-être que j'aurais trop dit alors ) :
Montrer que :
 ^2 }{4})
Normalement devant un tel exercise on doit connaitre cette inegalite d'avance ou bien la trouver (pas connu d'avance ni meme ecrite dans l'enonce) pour le resoudre ?

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 18 Nov 2009, 13:15
par Olympus » 18 Nov 2009, 13:15
Qmath a écrit:Normalement devant un tel exercise on doit connaitre cette inegalite d'avance ou bien la trouver (pas connu d'avance ni meme ecrite dans l'enonce) pour le resoudre ?
La trouver, il n'y a pas de questions intermédiaires, mais faut quand même se dire que la première des choses à faire c'est d'encadrer
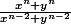
en expérimentant un peu avec Chebyshev

-
Anonyme
 par Anonyme » 18 Nov 2009, 14:09
par Anonyme » 18 Nov 2009, 14:09
Olympus a écrit:La trouver, il n'y a pas de questions intermédiaires, mais faut quand même se dire que la première des choses à faire c'est d'encadrer
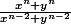
en expérimentant un peu avec Chebyshev

Oui j'ai penser a l'encadrer mais j'ai pa pu y arriver . Je ne connais pas Chebyshev donc bon ... Peux tu me montrer comment tu l'a trouver ?

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 18 Nov 2009, 15:19
par Olympus » 18 Nov 2009, 15:19
En appliquant l'inégalité de Chebyshev sur les deux suites
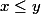
et
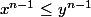
, on a :
 \geq \left(x+y \right) \left( x^{n-1} + y^{n-1} \right))
(i)
En appliquant, une deuxième fois, l'inégalité de Chebyshev sur les deux suites
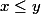
et
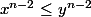
:
 \left( x^{n-2} + y^{n-2} \right) }{2})
(ii) .
De (i) et (ii) :
 \geq \frac{ \left( x+y \right) ^2 \left(x^{n-2} + y^{n-2} \right) }{2})
 ^2 }{4})
Puis vient le job de Cauchy-Schwarz qui permet de conclure l'inégalité recherchée

-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 18 Nov 2009, 17:36
par benekire2 » 18 Nov 2009, 17:36
Quasiment les deux inégalités les plus utilisées en OIM ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 18 Nov 2009, 17:37
par benekire2 » 18 Nov 2009, 17:37
Je te souhaite de réussir demain olympus :)

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 18 Nov 2009, 17:40
par Olympus » 18 Nov 2009, 17:40
benekire2 a écrit:Je te souhaite de réussir demain olympus

Merci

Mais je sens que je vais foirer tout en géométrie x'(
Ah mais c'est après-demain les olympiades de Kénitra, mais c'est vrai que demain je pourrais pas réviser ^^

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 18 Nov 2009, 18:07
par Olympus » 18 Nov 2009, 18:07
Bon je termine la démo .
Donc :
 ^2 + \left( y+z \right) ^2 + \left( z+x \right)^2 }{4})
(iii)
Selon l'inégalité de Cauchy-Schwartz :
 ^2 + \left( y+z \right) ^2 + \left( z+x \right)^2 \right) \geq \left( \left( x+y \right) + \left( y+z \right) + \left( z+x \right) \right)^2)
 ^2 + \left( y+z \right) ^2 + \left( z+x \right)^2 \geq \frac{4}{3} \left( x+y+z \right) ^2)
.
 ^2 + \left( y+z \right) ^2 + \left( z+x \right)^2 \geq \frac{4}{3})
(iv)
de (iii) et (iv) on conclut l'inégalité recherchée !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
en expérimentant un peu avec Chebyshev