Limites trigo ardues
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 23 Oct 2010, 13:18
par froudjik » 23 Oct 2010, 13:18
Bonjour, j'ai deux limites que je ne sais pas trop comment déterminer. Merci de m'aider svp

1ère :
\])
2ème :
}\)\])
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 23 Oct 2010, 13:24
par froudjik » 23 Oct 2010, 13:24
Pour la première j'ai un peu simplifié l'expression, je sais pas si ça peut aider :
J'ai :
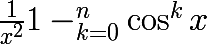=\frac{1}{x^2}(1-cos^{\frac{n(n+1)}{2}}{x}))
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 23 Oct 2010, 15:47
par froudjik » 23 Oct 2010, 15:47
svp... :hein:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 23 Oct 2010, 15:50
par Ericovitchi » 23 Oct 2010, 15:50
Pour la seconde regardes
là ou
là si tu veux, c'est assez classique.
la première tends vers n(n+1)/4 en faisant des développements limités (ou avec la règle de l'hospital)
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 23 Oct 2010, 16:58
par froudjik » 23 Oct 2010, 16:58
Merci beaucoup de ta réponse !
Je ne suis qu'en terminale, je n'ai pas encore vu les développements limités. Je vais essayer avec la règle de l'Hospital...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 23 Oct 2010, 17:11
par Ericovitchi » 23 Oct 2010, 17:11
Oui la règle de l'hospital marche très bien dans ce cas. Tu as juste à savoir que sin x / x tend vers 1 pour trouver que c'est la moitié de l'exposant, la limite.
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 23 Oct 2010, 18:45
par froudjik » 23 Oct 2010, 18:45
Sur
ce site ils parlent d'une méthode qui n'utilise pas la règle de l'hospital mais je ne comprends pas la dernière étape quand ils passent de l'expression de la limite à
}{2})

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Oct 2010, 20:41
par Sa Majesté » 23 Oct 2010, 20:41
Salut
Tu as

Et
 = k = \frac{n(n+1)}{2})
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 23 Oct 2010, 20:47
par froudjik » 23 Oct 2010, 20:47
Sa Majesté a écrit:Et
 = k)
J'imagine que c'était

Mais c'est justement ça que je ne comprends pas...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Oct 2010, 21:44
par Ben314 » 23 Oct 2010, 21:44
Salut,
Heuuuu, c'est moi qui suis con ou bien, l'énoncé tel quel avec k qui commence à 0 est franchement couillon ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 23 Oct 2010, 23:20
par muse » 23 Oct 2010, 23:20
lim cos(x)=1 quand x tend vers 0 et 1 puissance k ça fera toujours 1
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 24 Oct 2010, 16:59
par froudjik » 24 Oct 2010, 16:59
Ah oui je suis c** ! Merci beaucoup :)
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 26 Oct 2010, 20:06
par froudjik » 26 Oct 2010, 20:06
Rebonjour,
Désolé, je suis un boulet je sais, mais pour revenir sur un des lien qu'a posté Ericovitchi, je ne comprends pas ce calcul :
f' (x) = sin(x)cos(2x) ..cos(nx) + cos(x)2sin(2x)...cos(nx) +... +cos(x)cos(2x)...nsin(nx)
Un équivalent de f' (x) est donc: ( 1² + 2² +... + n² ) * x
Quand il parle d'equivalent, ca veut dire que la limite en 0 est la même ?
Dans ce cas je ne comprends pas comment on peut conclure à partir de ça. On pourrait donner n'importe quoi comme expression à
Je vois juste que comme il y a des sin partout, forcément la limite de f' en 0 sera 0, mais ca ne m'avance pas beaucoup ça...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Oct 2010, 20:32
par Sa Majesté » 26 Oct 2010, 20:32
Il utilise la règle de l'Hopital
Le numérateur vaut sin(x)cos(2x) ..cos(nx) + cos(x)2sin(2x)...cos(nx) +... +cos(x)cos(2x)...nsin(nx)
Chacun des cos est équivalent à 1 en 0
Chacun des sin(kx) est équivalent à kx
Du coup le numérateur est équivalent à x+4x+ ... + n²x = (1+4+...+n²)x
Le dénominateur vaut 2x
Le ratio est équivalent à (1+4+...+n²)x / (2x) = (1+4+...+n²)/2 = n(n+1)(2n+1)/12
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 26 Oct 2010, 20:51
par froudjik » 26 Oct 2010, 20:51
Chacun des sin(kx) est équivalent à kx
Mais que veut dire "equivalent" exactement ?
On ne voit pas vraiment cette notion au lycée pour calculer des limites si ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 26 Oct 2010, 20:52
par Sa Majesté » 26 Oct 2010, 20:52
froudjik a écrit:On ne voit pas vraiment cette notion au lycée pour calculer des limites si ?
Non je ne pense pas
C'est lié aux développements limités
A mon avis tu peux laisser tomber sauf si tu veux approfondir par curiosité
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 26 Oct 2010, 23:00
par froudjik » 26 Oct 2010, 23:00
Ce que je ne comprends pas, c'est que si on s'en tient au simple fait que cos(0)=1, la limite du numérateur revient à la limite de
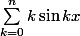
en 0 qui est 0*0+1*0+2*0+...+n*0=0
Or, le résultat attendu n'est pas du tout le même...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 27 Oct 2010, 11:12
par Sa Majesté » 27 Oct 2010, 11:12
Que la limite du numérateur soit égale à 0, je n'en disconviens pas
D'ailleurs quand on écrit qu'un équivalent au numérateur en 0 est (1+4+...+n²)x, on a bien 0 comme limite en 0
Le problème n'est pas de trouver la limite en 0 du numérateur car la limite du dénominateur est également 0 et on tombe sur une forme indéterminée
Le problème c'est de trouver un équivalent qui permette de lever cette indétermination
Ici on trouve comme équivalent en 0 : (1+4+...+n²)/2
Autre exemple
Si tu veux trouver la limite en 0 de (1-cos x)/sin x, tu peux utiliser la règle de l'Hôpital, ce qui donne sin x/cos x, ce qui fait 0 en 0
Avec les équivalents tu obtiens (x²/2) / x = x/2, dont la limite en 0 est 0. Tu obtiens même plus puisque tu peux dire que (1-cos x)/sin x se comporte comme x/2 au voisinage de 0
-
froudjik
- Membre Naturel
- Messages: 40
- Enregistré le: 27 Juin 2010, 23:07
-
 par froudjik » 27 Oct 2010, 13:20
par froudjik » 27 Oct 2010, 13:20
D'accord je crois que je comprends mieux...
Mais quelle est la méthode pour pour déterminer un équivalent au voisinage d'un point ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités