Exercicre sur les Déterminants.

[ashok]

Bonjour à tous,

je voudrais m'avancer dans les exos afin de mieux assimiler le cours, mais je me retrouve bloquer à un exercice..
Je vous cite l'énoncer :
"Soit n appartenant à {2;3} et A appartenant à Mn(R) telle que A²-A+In=0. Calculer A^3 et en déduire det A."

Je n'ai pas compris par où commencer du fait que n appartient à {2;3}..
si vous pouviez m'aider en me donnant les point à aborder, ou un quelconque aide, je suis preneur.

Merci d'avance à ceux qui répondrons à ma demande.

[Nightmare]

Salut,

A^3=A² x A = (A-In) x A = A²-A=-In

det(A^3)=...

[girdav]

Bonjour,
ici on regarde le problème pour les matrices de dimension 2 puis 3.
Ici, tu peux multiplier l'équation par pour faire apparaître le 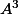. Ensuite tu te sers de l'équation de départ.
En fait, quand tu auras du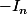 tu verras que l'intérêt de distinguer la dimension 2 de la dimension 3 est en fait celui de distinguer n pair de n impair.

[ashok]

Merci beaucoup pour votre aide j'ai bien compris l'exercice maintenant :)

après avoir calculer det A^3 comment trouver det A ?

Et j'ai un soucis aussi, car j'ai fait les calculs en dimension deux et c'est assez lourd, donc en dimension 3 j'imagine le pire :s
Ou alors je m'y suis mal pris dans la résolution du déterminant.

[ashok]

det A^3 = det A² x det A = det(A-In) x det A = det(-In)

en dimension deux j'ai poser A= [(a,b),(c,d)] comme matrice puis j'ai calculer det(-I2) = -1 et det A = ad-cb puis j'en déduis det A = -1/(ad-cb) = 1/(cb-ad)

je me suis tromper j'ai pas fait det (A-I2), il vaut ad - a - d + 1 - cb

Donc det A = -1/(ad -a - d + 1 - cb)