Défi : similitude, un point fixe
18 messages
- Page 1 sur 1
Défi : similitude, un point fixe
Bonsoir , voilà un défi qu'il nous faut relever en spémaths
malheureusement je ne vois pas vraiment sur quoi partir. Pourriez-vous m'aide svp ?
C1 et C2 deux cercles sécants en A et B
M1 et M2 deux points parcourant dans le meme sens C1et C2, chacun avec une vitesse angulaire constante.
A chause tour M1 ET M2 passent en meme temps en A.
Demontrer qu'il existe un point fixe équidistant constamment de M1 et M2.
J'essaie d'xprimer la vitesse angulaire de l'un en fonction de l'autre, c'est à dire en fonction du rapport entre kes rayons R1/R2.
Mais ça ne me mène pas loin. M^me s'il me semble qu'on pourrait alors de cette manière trouver l'emplacement de M2 par rapport à M1, ce qui nous permettrait, en répétant cette opération plusieurs fois d'obtenir le point invariant, mais je ne sais absolument pas à quoi m'en tenir et comment partir et mettre cela en forme.
Merci beaucoup.
malheureusement je ne vois pas vraiment sur quoi partir. Pourriez-vous m'aide svp ?
C1 et C2 deux cercles sécants en A et B
M1 et M2 deux points parcourant dans le meme sens C1et C2, chacun avec une vitesse angulaire constante.
A chause tour M1 ET M2 passent en meme temps en A.
Demontrer qu'il existe un point fixe équidistant constamment de M1 et M2.
J'essaie d'xprimer la vitesse angulaire de l'un en fonction de l'autre, c'est à dire en fonction du rapport entre kes rayons R1/R2.
Mais ça ne me mène pas loin. M^me s'il me semble qu'on pourrait alors de cette manière trouver l'emplacement de M2 par rapport à M1, ce qui nous permettrait, en répétant cette opération plusieurs fois d'obtenir le point invariant, mais je ne sais absolument pas à quoi m'en tenir et comment partir et mettre cela en forme.
Merci beaucoup.
Tu cherche une preuve uniquement "géométrique" ou tu accepte de faire des calculs (coordonnées) ?
Dans le second cas, c'est pas trop trop complexe, mais dans le premier cas, ça me semble assez "chaud" (la seule soluce que j'ai est assez longue...)
Dans le second cas, c'est pas trop trop complexe, mais dans le premier cas, ça me semble assez "chaud" (la seule soluce que j'ai est assez longue...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour ce qui est de la vitesse, je ne vois pas ce que je pourrais vraiment savoir, puisque la vitesse est V= D/T avec D= 2Pi R , sachant que les cercles ne sont pas les mêmes. Je peux juste dire que la vitesse de l'un est R1/R2 * Vitesse de l'autre.
Par contre, je ne cherche pas de méthode précise, que ce soit avec du qualitatif , des complexes ou des coordonnées cartésiennes, je ne vois aucun problème.
La seule chose est que je ne sait pas sur quoi partir.
Par contre, je ne cherche pas de méthode précise, que ce soit avec du qualitatif , des complexes ou des coordonnées cartésiennes, je ne vois aucun problème.
La seule chose est que je ne sait pas sur quoi partir.
Il me semble que c'est plus façile à trouver par du calcul (si j'ai un peu de temps, je te donnerais une preuve "pure géométrique"...)
Perso, quitte à changer l'échelle, je me placerais dans un repère centré en O1 (centre de C1) tel que que le point A ait pour affixe 1 (donc que C1 ait pour rayon 1)
Le point mobile M1 a à l'instant t pour affixe m1=exp(it) [en considérant que t=0 <-> M1=A et que la vitesse angulaire est 1]
Si on note omega l'affixe de O2 (centre de C2) et si on écrit 1=omega+r.exp(i.alpha) [donc r=rayon de C2] le point M2 a pour affixe m2=omega+r.exp(i.(alpha+t)) [en considérant que t=0 <-> M2=A et que la vitesse angulaire est 1].
Essaye de simplifier l'expression de m2, puis cherche une équation de la médiatrice de [M1M2] (qui dépend de t) et enfin montre qu'il existe un (unique) point qui est sur toutes les médiatrices...
Bon courage...
Perso, quitte à changer l'échelle, je me placerais dans un repère centré en O1 (centre de C1) tel que que le point A ait pour affixe 1 (donc que C1 ait pour rayon 1)
Le point mobile M1 a à l'instant t pour affixe m1=exp(it) [en considérant que t=0 <-> M1=A et que la vitesse angulaire est 1]
Si on note omega l'affixe de O2 (centre de C2) et si on écrit 1=omega+r.exp(i.alpha) [donc r=rayon de C2] le point M2 a pour affixe m2=omega+r.exp(i.(alpha+t)) [en considérant que t=0 <-> M2=A et que la vitesse angulaire est 1].
Essaye de simplifier l'expression de m2, puis cherche une équation de la médiatrice de [M1M2] (qui dépend de t) et enfin montre qu'il existe un (unique) point qui est sur toutes les médiatrices...
Bon courage...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Dit comme ça , ça paraît assez simpe,
mais déjà à ce début, il ya quelques difficultés qui surviennent.
Car je trouve
m2= omega + r e^(i*alpha)+ re^(it)
m2= 1 + r m1
non ? Je vois mal comment le simplifier d'autre.
Mais alors pour calculer une équation de la médiatrice, là j'avoue j'ai un gros problème car il faut forcément calculer d'abord l'éqaution de (M1M2) et partir sur z=x+yi non?
et j'ai m1= e^(it) et m2=1+r*e^(it)
je veux bien repasser à l'écriture algébrique mais j'ai des cos(t) + i sin(t) !
alors je ne vois pas vraiment,
et par contre pour calculer la médiatrice, une fois qu'on a l'équation de la droite, je n'ai pas vraiment d'idée, à part trouver le milieu et calculer un vecteur normal, ou utiliser le produit scalaire, mais je n'arriverai pas à une équation de droite alors ?
Comment faire ?
mais déjà à ce début, il ya quelques difficultés qui surviennent.
Car je trouve
m2= omega + r e^(i*alpha)+ re^(it)
m2= 1 + r m1
non ? Je vois mal comment le simplifier d'autre.
Mais alors pour calculer une équation de la médiatrice, là j'avoue j'ai un gros problème car il faut forcément calculer d'abord l'éqaution de (M1M2) et partir sur z=x+yi non?
et j'ai m1= e^(it) et m2=1+r*e^(it)
je veux bien repasser à l'écriture algébrique mais j'ai des cos(t) + i sin(t) !
alors je ne vois pas vraiment,
et par contre pour calculer la médiatrice, une fois qu'on a l'équation de la droite, je n'ai pas vraiment d'idée, à part trouver le milieu et calculer un vecteur normal, ou utiliser le produit scalaire, mais je n'arriverai pas à une équation de droite alors ?
Comment faire ?
Bon, vu la façon de modéliser, le seul "paramètre" ici est le centre du cercle C2, c'est à dire omega.
Il faut donc essayer de tout exprimer en fonction de omega (et de t).
Comme 1=omega+r.exp(i.alpha), cela signifie que r.exp(i.alpha)=1-omega et donc que :
m2=omega+r.exp(i.(alpha+t))
=omega+r.exp(i.alpha).exp(it)
=omega+(1-omega).exp(it)
Ensuite, effectivement, niveau Lycée, il vaut sans doute mieux écrire les coordonnées de M1 et M2 pour trouver l'équation de la médiatrice.
m1=exp(it) donc M1:(cos(t),sin(t))
m2=omega+(1-omega).exp(it) donc M2:(...,...) en considérant que omega=a+ib.
Une fois les coordonnées de M1 et M2 obtenues, pour trouver l'équation de la médiatrice, tu peut effectivement calculer le millieu de [M1M2] et dire que le vecteur vect(M1M2) est un vecteur normal à la droite.
Tu doit obtenir une équation de la forme ?x+?y+?=0 où les ? dépendent de t (et de a et b).
Il restera à trouver un point (x,y) dont les coordonnées ne dépendent que de a et b (et pas de t) qui vérifie l'équation ?x+?y+?=0 pour toutes les valeurs de t...
Il faut donc essayer de tout exprimer en fonction de omega (et de t).
Comme 1=omega+r.exp(i.alpha), cela signifie que r.exp(i.alpha)=1-omega et donc que :
m2=omega+r.exp(i.(alpha+t))
=omega+r.exp(i.alpha).exp(it)
=omega+(1-omega).exp(it)
Ensuite, effectivement, niveau Lycée, il vaut sans doute mieux écrire les coordonnées de M1 et M2 pour trouver l'équation de la médiatrice.
m1=exp(it) donc M1:(cos(t),sin(t))
m2=omega+(1-omega).exp(it) donc M2:(...,...) en considérant que omega=a+ib.
Une fois les coordonnées de M1 et M2 obtenues, pour trouver l'équation de la médiatrice, tu peut effectivement calculer le millieu de [M1M2] et dire que le vecteur vect(M1M2) est un vecteur normal à la droite.
Tu doit obtenir une équation de la forme ?x+?y+?=0 où les ? dépendent de t (et de a et b).
Il restera à trouver un point (x,y) dont les coordonnées ne dépendent que de a et b (et pas de t) qui vérifie l'équation ?x+?y+?=0 pour toutes les valeurs de t...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Mais est-ce que là , on sort du repère complexe et on passe dans un repère cartésien si omega=a+by ? ça sort d'où exactement , je veux dire qu'est-ce que c'est comme coordonnée en fait ? Est-ce qu'on ne peut pas garder les complexes avec omega = a+bi ?
mais à ce mùoment là, le exp(it) est-ce qu'on le garde tel quel, parce que moi je sais juste trouver les coordonées cartésiennes à parti de l'affixe : ça veut dire que pour faire mon calmavul, je part d'abord sur omega= a+bi, je fais mon calcul pour obtenir m2
j'ai : m2=(a+cost-acost+bsint) + (b+sint-bcost-asint)i et là j'ai
M2: (a+cost-acost+bsint ; b+sint-bcost-asint). Non ?
jusque là, est-ce que ça va ?
j'obtiendrais alors, (d)=médiatrice de [M1M2]
(d) : (a-acost+bsint)x +(b-bcost-asint)y +c=0
pour déterminer c, il faut un point
je suppose qu'on peut partir du fait que A appartient à la médiatrice puisque M1 et M2 sont confondus en A, si t=0, mais à ce moment là, ce ne sra pas l'équation de la médiatrice , QUel Que SOit t., e-t ce sera UNE médiatrice , celle de t=0.
Est-ce qu'il faudrait plutôt déterminer c en disant que (d) passe par I le mileu de [M1M2], dont on peut facilement calculer les coordonées ?
Mais après, le calcul est extrêment long, et il ne faut pas se tromper, mais est-ce qu'il se simplifie, ou est-ce qu'il faut ne pas développer ?
mais à ce mùoment là, le exp(it) est-ce qu'on le garde tel quel, parce que moi je sais juste trouver les coordonées cartésiennes à parti de l'affixe : ça veut dire que pour faire mon calmavul, je part d'abord sur omega= a+bi, je fais mon calcul pour obtenir m2
j'ai : m2=(a+cost-acost+bsint) + (b+sint-bcost-asint)i et là j'ai
M2: (a+cost-acost+bsint ; b+sint-bcost-asint). Non ?
jusque là, est-ce que ça va ?
j'obtiendrais alors, (d)=médiatrice de [M1M2]
(d) : (a-acost+bsint)x +(b-bcost-asint)y +c=0
pour déterminer c, il faut un point
je suppose qu'on peut partir du fait que A appartient à la médiatrice puisque M1 et M2 sont confondus en A, si t=0, mais à ce moment là, ce ne sra pas l'équation de la médiatrice , QUel Que SOit t., e-t ce sera UNE médiatrice , celle de t=0.
Est-ce qu'il faudrait plutôt déterminer c en disant que (d) passe par I le mileu de [M1M2], dont on peut facilement calculer les coordonées ?
Mais après, le calcul est extrêment long, et il ne faut pas se tromper, mais est-ce qu'il se simplifie, ou est-ce qu'il faut ne pas développer ?
Oui, c'est exactement ça : tu garde les complexes tant que les calculs sont plus simples en complexes, puis, lorsque tu veut l'équation de la médiatrice que tu aimerais avoir sous la forme "usuelle" ?x+?y+?=0, tu revient en coordonnées "usuelles"
Effectivement, pour omega=a+by, c'est une faute de frappe : il fallait lire "omega=a+bi"
les réels a et b sont les coordonnées du centre O2 et donc il faut les voir dans les calculs comme des paramètres (comme quand on te dit "la droite d'équation y=ax+b" ou "le polynôme P(X)=ax²+bx+c")
Donc tu aura des 'a' et des 'b' jusqu'à la fin des calculs et les coordonnées du point qui est sur toutes les médiatrices dépendra de a et b ce qui signifie que ce point dépend de la position de O2 (ce qui n'est pas étonant)
Effectivement, pour omega=a+by, c'est une faute de frappe : il fallait lire "omega=a+bi"
les réels a et b sont les coordonnées du centre O2 et donc il faut les voir dans les calculs comme des paramètres (comme quand on te dit "la droite d'équation y=ax+b" ou "le polynôme P(X)=ax²+bx+c")
Donc tu aura des 'a' et des 'b' jusqu'à la fin des calculs et les coordonnées du point qui est sur toutes les médiatrices dépendra de a et b ce qui signifie que ce point dépend de la position de O2 (ce qui n'est pas étonant)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Tout ce que tu vient de rajouter (pendant que je tapais) est O.K.
Ton équation me semble correcte (je n'ai pas vérifié) et effectivement, pour trouver le 'c' de cette équation, il faut utiliser les coordonnées du millieu de [M1,M2].
Tu constae que cette méthode est quand même trés calculatoire.
Elle ne demande pas trop d'imagination mais... il ne faut pas se gourrer dans les calculs...
C'est une des raisons pour lesquelles on préfère les méthodes "purement géométriques" (mais il faut avoir de l'intuition pour savoir par quel bout s'y prendre...)
Ton équation me semble correcte (je n'ai pas vérifié) et effectivement, pour trouver le 'c' de cette équation, il faut utiliser les coordonnées du millieu de [M1,M2].
Tu constae que cette méthode est quand même trés calculatoire.
Elle ne demande pas trop d'imagination mais... il ne faut pas se gourrer dans les calculs...
C'est une des raisons pour lesquelles on préfère les méthodes "purement géométriques" (mais il faut avoir de l'intuition pour savoir par quel bout s'y prendre...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je confirme, c'est très, calculatoire...
Je trouve finalement :
c= (a²-a+b²)cos(t) -bsin(t) - a²+a-b²
et donc
(d) : (a-acos(t)+bsin(t))x +(b-bcos(t)-asin(t))y + c = 0
C'est joli...
Par contre, je ne vois pas, mais alors pas du tout, comment on détermine le point qui ne dépende pas de t.
Si t=0, on a bien 0=0
( je sais juste, grâce à geogebra, que ce point est le 4° sommet du parallélogramme O1 O2 B et gamma , le point cherché.
(Car, sur la pseudo figure qui nous est donnée, on a la droite (M1M2) passant par B : etb d'ailleurs c'st ce que je ne comprned pas pourquoi) )
Je trouve finalement :
c= (a²-a+b²)cos(t) -bsin(t) - a²+a-b²
et donc
(d) : (a-acos(t)+bsin(t))x +(b-bcos(t)-asin(t))y + c = 0
C'est joli...
Par contre, je ne vois pas, mais alors pas du tout, comment on détermine le point qui ne dépende pas de t.
Si t=0, on a bien 0=0
( je sais juste, grâce à geogebra, que ce point est le 4° sommet du parallélogramme O1 O2 B et gamma , le point cherché.
(Car, sur la pseudo figure qui nous est donnée, on a la droite (M1M2) passant par B : etb d'ailleurs c'st ce que je ne comprned pas pourquoi) )
Effectivement, prendre deux valeurs différentes pour t et résoudre les deux équations marcherais, mais il y a un peu plus simple :
L'équation de la médiatrice est :
(a-acos(t)+bsin(t))x +(b-bcos(t)-asin(t))y + (a²-a+b²)cos(t) -bsin(t) - a²+a-b²=0
Tu cherche un couple (x,y) qui vérifie cette formule pour toutes les valeur de t.
Il peut venir à l'esprit de réécrire l'équation sous la forme :
? + ?.cos(t) + ?.sin(t) = 0
où les trois '?' ne contiennent pas de t.
Evidement, s'ils sont tout les trois nuls alors la formule est valable pour tout réel t...
L'équation de la médiatrice est :
(a-acos(t)+bsin(t))x +(b-bcos(t)-asin(t))y + (a²-a+b²)cos(t) -bsin(t) - a²+a-b²=0
Tu cherche un couple (x,y) qui vérifie cette formule pour toutes les valeur de t.
Il peut venir à l'esprit de réécrire l'équation sous la forme :
? + ?.cos(t) + ?.sin(t) = 0
où les trois '?' ne contiennent pas de t.
Evidement, s'ils sont tout les trois nuls alors la formule est valable pour tout réel t...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
D'accord!! On obtient finalement les coordonées du point fixe en réolvant le système des 3 ? en fonction de a, b et c. ça marche, ça donne de jolies coordonées.
Et bien finalement ça a été laborieux. Merci infiniment Ben314
Et c'st vrai que finalement le dessin géométrique est bien plus joli et semble en fait bien plus simple.
En partant de la construction après on doit bien arriver à trouver une démonstration et on peut même y ajouter des similitudes à étudier.
Par contre en fait je ne vois pas exactement dans quel ordre ('par quoi tu as commencé) tu es arrivé à construire le point A' ?
encore merci
Et bien finalement ça a été laborieux. Merci infiniment Ben314
Et c'st vrai que finalement le dessin géométrique est bien plus joli et semble en fait bien plus simple.
En partant de la construction après on doit bien arriver à trouver une démonstration et on peut même y ajouter des similitudes à étudier.
Par contre en fait je ne vois pas exactement dans quel ordre ('par quoi tu as commencé) tu es arrivé à construire le point A' ?
encore merci
Le dessin sous entend que, en faisant quelques essais, tu as déjà conjecturé (i.e tu pense que) le point commun à toutes les médiatrices de  est le symétrique
est le symétrique  de
de 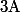 par rapport à la médiatrice de
par rapport à la médiatrice de  . Il reste donc à démontrer que ce fameux point
. Il reste donc à démontrer que ce fameux point  est bien sur la médiatrice de
est bien sur la médiatrice de  quelque soit la position du point
quelque soit la position du point  .
.
Dans le dessin, on construit donc ce fameux point , on prend pour
, on prend pour  un point au pif sur le cercle
un point au pif sur le cercle  et on prend
et on prend  sur
sur  tel que l'angle (orienté)
tel que l'angle (orienté) ) soit égal à
soit égal à ) (angles verts de la figure) pour traduire que les vitesse angulaires des deux points sont les mêmes.
(angles verts de la figure) pour traduire que les vitesse angulaires des deux points sont les mêmes.
Il faut alors démontrer que les longueurs et
et  sont forcément égales.
sont forcément égales.
La figure contient des information (couleurs des angles, de certain triangles...) qu'il faut petit à petit démontrer en partant des deux hypothèses pour finalement arriver au résultat...
P.S. Pour la partie "calculs", en fait le choix de départ de prendre O1:(0,0) A:(1,0) et O2(a,b) n'était en fait pas judicieux (c'est normal, vu que c'est moi qui l'ai suggéré...) : tu as trouvé les coordonnées du point fixe, mais, vu ces coordonnées, on ne voit pas trop où il est situé par rapport à O1, O2 et A.
Vu le résultat, il aurait été plus judicieux de partir de O1:(-1,0) ; O2:(1,0) et A(a,b) : les calculs auraient été à peu prés les mêmes, mais on aurait obtenu comme point fixe des médiatrices le point (-a,b) ce qui été trés facilement interprétable en terme "géométrique"...
Dans le dessin, on construit donc ce fameux point
Il faut alors démontrer que les longueurs
La figure contient des information (couleurs des angles, de certain triangles...) qu'il faut petit à petit démontrer en partant des deux hypothèses pour finalement arriver au résultat...
P.S. Pour la partie "calculs", en fait le choix de départ de prendre O1:(0,0) A:(1,0) et O2(a,b) n'était en fait pas judicieux (c'est normal, vu que c'est moi qui l'ai suggéré...) : tu as trouvé les coordonnées du point fixe, mais, vu ces coordonnées, on ne voit pas trop où il est situé par rapport à O1, O2 et A.
Vu le résultat, il aurait été plus judicieux de partir de O1:(-1,0) ; O2:(1,0) et A(a,b) : les calculs auraient été à peu prés les mêmes, mais on aurait obtenu comme point fixe des médiatrices le point (-a,b) ce qui été trés facilement interprétable en terme "géométrique"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
En fait on se rend comte qu'une fois qu'on sait où l'on va et ce que l'on veut exactement prouver c'est à dire une fois qu'on a un bon dessin, c'est quand même bien plus simple.
Du moins ma démonstration géométrique qui prouve que A' appartient à la médiatrice de [M1M2] tient en quelques lignes alors que la partie calculs faisait une page et demi !
J'ai refait la partie calculs, et on obtient bien , par la même méthode que A' est le symétrique de A par rapport à la droite : donc ça marche !
Merci infiniment Ben 314, je ne sais pas ce que j'aurais fait sans toi. :we:
Du moins ma démonstration géométrique qui prouve que A' appartient à la médiatrice de [M1M2] tient en quelques lignes alors que la partie calculs faisait une page et demi !
J'ai refait la partie calculs, et on obtient bien , par la même méthode que A' est le symétrique de A par rapport à la droite : donc ça marche !
Merci infiniment Ben 314, je ne sais pas ce que j'aurais fait sans toi. :we:
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 132 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

