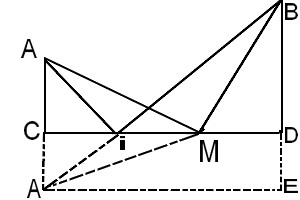
Un élastique fixé en A et B

[Agrypnos]

J'aurais besoin de conseil pour effectuer mon devoir maison.

Un élastique fixé en A et B passe dans un anneau qui coulisse entre C et D.
Le but de cet exercice est d'étudier les variations de la longueur de cet élastique suivant la position de M sur le segment [CD].

1) Refaire la figure ci-dessus et mesurer la longueur "l" de l'élastique lorsque X vaut 0 ; 1 ; 2 ; 3.
Compléter alors le tableau suivant :

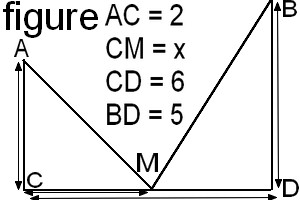
x | 0 1 2 3
l=AM+MB |

2) a) Exprimer AM en fonction de x.
b) Exprimer MB en fonction de X.
c) En déduire la longueur l = AM + MB en fonction de x.
d) Vérifier les valeurs mesurées dans la question 1).

3) a) Quel est l'ensemble des nombres x possibles?
b) Observer la représentation graphique de la fonction x[smb]fleche2[/smb]l sur une calculatrice. Déterminer alors,
avec la calculatrice, une valeur approchée à 0,1 près du maximum et celle du minimum de cette fonction.

4) a) Dresser un tableau de valeurs de la fonction x[smb]fleche2[/smb]l sur l'intervalle [1 ; 2] avec un pas de 0,1.
En déduire une valeur approchée de x à 0,1 près pour laquelle la longueur l est minimale.
b) Dresser un tableau de valeurs de cette même fonction sur l'intervalle [1,7 ; 1,8] avec un pas de 0,01.
En déduire une valeur approchée de X à 0,01 près pour laquelle la longueur l est minimale.


Je suis tout ouï pour des conseils ou aides.
Merci d'avance!


réponse du 1)
pr x = 0 d'après pyth. => l² = 4 + 121 => l = racine(125)
pr x = 1 d'après pyth. => l² = 9 + 100 => l = racine(109)
pr x = 2 d'après pyth. => l² = 16 + 81 => l = racine(97)
pr x = 3 d'après pyth. => l² = 25 + 64 => l = racine(89)
réponse du 2)
a) AM² = CA² + CM² => AM = r((4+x²))
réponse du 2)
b) MB² = MD² + DB² => MB² = (6-x)² + 25 => MB = r((6-x)² + 25)
c) AM + MB = r(4+x²) + r((6-x)² + 25)
réponse du 2)
d) l=0 r(4) + r(36 + 25)
...

Et c'est à partir de là où je bloque, d'où vient mon problème? Merci d'avance!

[Lostounet]

a) AM² = CA² + CM² => AM = (4+x²)

Et c'est à partir de là où je bloque, d'où vient mon problème? Merci d'avance!

:hein:
En assumant que le triangle est rectangle.
D'après le théorème de Pythagore, on a:
AM² = AC² + CM²
AM² = 2² + x²
AM² = 4 + x²
AM = (4 + x²).. :hein:

[Agrypnos]

Ouais ouais j'ai écris trop vite! :we:
Sinon tu n'as pas une ptite idée?

[Benjamin]

Bonjour,

A la question 1, on te demande de mesurer, et non pas de faire les calculs. De plus, tes calculs en 1 sont faux. Tu as l=AM+MB ce qui n'est pas du tout équivalent à l²=AM²+MB² !! (le calcul que tu as fait...) l²=AM²+MB²+2*AM*MB . Et, tu as mal utiliser Pythagore l²=a²+b² et non pas (a+b)².

Tu as donc 2 erreurs. Mais, comme je le disais, on te demande juste de mesurer pour cette question.

[Lostounet]

b) Exprimer MB en fonction de X.
b) MB² = MD² + DB² => MB² = (6-x)² + 25 => MB = r((6-x)² + 25)

Dans le triangle MBD, rectangle en D. On a, d'après le théorème de Pythagore:
MB² = MD² + BD²
MB² = (6 - x)² + 5² (La réponse que tu as obtenue est donc juste)
Pourquoi ne pas simplifier un peu, en développant?

MB² = 36 - 12x +....
MB² = ...
MB = (...)

l = MB + AM
l = .... + (4 + x²)

[Agrypnos]

merci j'ai pu réfléchir et répondre à toute les questions maintenant je bloque dans la deuxième partie :

5)A' est le symétrique de A par rapport à (CD)
a) Justifier l'égalité : A'M + MB = l
b) Pour quelle position de M sur [CD] a-t-on la longueur l la plus petite?
c) A l'aide du théorème de Thalès calculer la valeur exacte du nombre x (notée x0) pour laquelle l est minimale.
d) Calculer la valeur exacte du minimum, notée l0, de la fonction x |--> l

6) a) dresser le tableau de vaiation de la fonction x |--> l avec des valeurs exactes
b) En utilisant une feuille de papier millimétré, (en prenant 2 cm pour l'unité sur l'axe des abscisses et sur l'axe des ordonnées), représenter graphiquement la fonction x |--> l.

[Agrypnos]

up!!!!!!!!

[Ericovitchi]

tu vois bien que CM est la médiatrice de AA' donc MA=MA' et donc on peut remplacer AM+BM par MA'+BM

Quand est-ce que la longueur A'MB sera la plus courte à ton avis ?
Quand les points sont alignés pardi (la ligne droite est le plus court chemin d'un point à un autre).
Essayes de réfléchir et de trouver des réponses par toi même, il n'y a guère de difficultés.

[Agrypnos]

Merci j'ai avancé mais je suis bloqué à la 5)C) !

[Ericovitchi]

On t'indique qu'il faut que tu appliques Thales entre les deux triangles DMB et CMA' (dans la configuration où les points BMA' sont alignés évidemment) alors essayes.

[Agrypnos]

jeb trouve pas :triste:

[Ericovitchi]

MC/MD=AC/BD --> x/(6-x)= 2/5 et tu trouves x

[Agrypnos]

oki c'est trouvé merci!
maintenant je bloque sur la 5) D) :(

[Ben314]

P'tèt ben qu'un petit coup de Pythagore...