Application du produit scalaire

[liliou]

voilà je ne comprend pas très bien comment faire cette exercice :
je bloque car on ne connait pas a et b voici l'ennoncé :

Dans un plan muni d'un repère ( O,i, j) on considère une droite d'équation (D) d'équation ;
ax + by + c = 0

Soit A ( xa : ya ) un point quelconque du plan et H son projeté orthogonal sur la droite (D)

1) Donner les coordonnées d'un vecteur normal a la droite (D)

2) Démontrer qu'il existe une réel k tel que :

xh = xa +ka et yh = ya + kb

merci d'avance pour votre aide

[Arnaud-29-31]

Bonjour,

Peux tu déjà donner un vecteur normal à la droite (D) ? Ca doit être dans ton cours ça ...

[liliou]

j'ai mi :
Soit le vecteur u de coordonnée (a, b) normal a (D)
et j'ai posé une seconde droite perpendiculaire à D tel que a'x + b'y + c = 0
d est perpendiculaire à Delta si et seulement si aa' + bb' = 0
on cherche donc un couple tel que (a' ; b') mais après je ne sais pas comment faire vu que je n'ai pas de nombre, je ne vois pas du tout comment je peux résoudre

[Arnaud-29-31]

Oui le vecteur normal, (on va plutôt l'appeler n) est de coordonnées :

Ensuite on a H qui est le projeté orthogonale de A sur (D), que peut-on donc dire de ?

[liliou]

le vecteur AH est orthogonal a D mais je ne vois pas trop en quoi cela m'aide pour ses coordonnées ?

[liliou]

parce que je ne vois pas du tout comment faire

[Ericovitchi]

Comment sont tous les points M de la droites HA ?
Ils respectent par définition (puisque 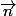est un vecteur directeur de la droite)

Notamment H est point particulier de cette droite donc il existe k tel que


Tu projettes sur les axes cette équation vectorielle :
ça donne
xh - xa = ka et yh - ya = kb et donc xh = xa +ka et yh = ya + kb

[liliou]

je n'ai donc pas de vrai valeur si je peux dire pour les coordonnées du vecteur n

[liliou]

enfaite, c'est bon j'ai compris merci,

[liliou]

cependant, après je dois déterminer les coordonnées de k mais comment je dois m'y prendre j'aimerais juste avoir une petite piste enfaite

[liliou]

euh désole c'est la valeur enfaite

[Ben314]

Lorsque tu as écrit (où plutôt Ericovitchi a écrit) que , tu as uniquement traduit le fait que H est sur la perpendiculaire à D passant par A (est ce clair ?)
Sauf que H n'est pas n'importe où sur cette perpendiculaire : il est ... donc ces coordonnées doivent vérifier ... ce qui permet de trouver la valeur de k (évidement en fonction de a,b,c,xa,ya)

Dans ce genre d'exo, il faut un peu "décoder" l'énoncé : tu fait comme si a,b,c,xa,ya étaient des "vrai nombres" que tu connais.

En fait si tu sait faire ce genre d'exo avec , ... (c'est à dire des valeurs "bizares") alors tu sait aussi le faire dans le cas général.

Personellement, je préfère le cas général, car pour faire 6x7 je me trompe souvent, alors que pour faire axb, ben là je me trompe pas , ça fait ab !!! :zen:

[liliou]

pourquoi H ne serais pas n'importe ou sur la perpendiculaire en effet, je dirais que h se trouve sur la droite que j'appellerai delta c'est à dire celle qui est perpendiculaire a D, je suis dans le vrai ou a coté de la plaque en disant ca ?

[liliou]

enfaite, on cherche le point d'intersection entre delta et D ??

[Ben314]

Oui, H doit aussi être sur la droite (D) de départ, donc les coordonnées de H (que tu vient d'exprimer en fonction de k) doivent vérivier l'équation de (D).
Tu devrait en déduire la valeur de k.

[liliou]

j'ai cherché la droite d'equation delta et je trouve quelque chose de bizzard : on sait que delta a pour vecteur normal u de coordonnées ( -b ; a ) et passe par A a partir de la je trouve delta : -bxa + aya + c = 0
mais ne devrais je pas trouver axa + bya + c = 0 ??
a vrai dire je crois je capte rien mais bn

[liliou]

enfaite, j'ai fait autre chose :
soit (D) ax +by + c = 0
A ( xa ; ya ) est un point quelconque
et H appartient à D
le vecteur AH a pour coordonnées ( x - xa ; y - ya )
AH.n = ( x - xa )a + ( y - ya ) = 0
= ax - axa + by - bya

comme h appartient à D ses coordonnées doiivent vérifier l'équation
axh - axa + byh - bya = 0

je ne sais pas comment expliquer ce changement d'écriture!
axh + byh + c = 0

ainsi on trouve AH.n = axa + bya + c = 0

mais après je ne sais pas comment faire pour trouver la valeur de k !
:help:

[liliou]

QU'est ce que vous en pensez ?

[Ben314]

Tu est en train d'aller à toute vitesse... en marche arrière.
Le vecteur n est un veterur normale de la droite de départ (D), c'est à dire qu'il est orthogonal à (D). Comme le vecteur AH est lui aussi orthogonale à (D), les vecteurs n et AH ne sont pas du tout perpendiculaires !!!! (en fait ils sont colinéaires) donc le produit scalaire n.AH n'est pas nul.

Tu as déjà montré que les coordonnées de H sont de la forme
xh = xa +k.a et yh = ya + k.b où k est un réel pour le moment inconnu.
Sauf que, pour établir cette relation, tu as écrit que le vecteur AH était perpendiculaire à (D) donc :
1) ce n'est pas la peine d'utiliser de nouveau le fait que AH est perpendiculaire à (D) : les coordonnées ci dessus le deisent déjà
2) Par contre, pour le moment on n'a pas utilisé le fait qu'on sait aussi que H est sur D, c'est à dire que ces coordonnées doivent vérifier l'équation de (D)...

[liliou]

JE N'ai jamais affirmer que le vecteur AH était orthogonal à n !
donc tu mon raisonnement n'est pas très bon ? parce que cela collerai vu qu'a la question suivante je dois trouver la distance AH .

:mur:

je ne vois pas trop a quoi ca m'avance, vu que je vais arrivé sur quelque chose du type axh + byh + c = 0