Isomorphismes

par **barbu23** » 09 Mar 2010, 20:05

Bonsoir, :happy3:
Soient

et

deux

- espaces vectoriels de dimensions respectivement :

et

.
Est ce que :

et

sont isomorphes ? :happy3:
Merci d'avance ! :happy3:

par **Doraki** » 09 Mar 2010, 20:09

Non, ils ont pas la même dimension.

par **barbu23** » 09 Mar 2010, 20:17

Oui, Merci d'abord, d'avoir repondu à ma question : :happy3:
Voiçi ce que je voulais dire : :happy3:
Existe - t - il un lien entre cette ecriture :

telle que :

et cette écriture :

tel que :

,
Quel lien y'a't-il entre

et

au niveau ensembliste c'est à dire :

et

mais, est ce qu'il existe un lien entre :

et

,
Merci d'avance ! :happy3:

par **barbu23** » 09 Mar 2010, 20:19

@Doraki :
Je viens de corriger mon premier poste ! donc à relire ! :happy3:

par **gnarfk** » 09 Mar 2010, 21:09

on va avoir un isomorphisme entre L( E , L(F,R )) et L(E , F). ces choses étant également isomorphes à l'ensemble formes bilinéaires sur ExF.

par **barbu23** » 10 Mar 2010, 12:53

Merci "gnarfk" pour ta reponse ! :happy3:
D'accord ! :happy3:
Et quel est l'isomorphisme qui permet de dire que ces deux ensembles sont isomorphes :

?
Merci d'avance ! :happy3:

par **Nightmare** » 10 Mar 2010, 13:01

Tu n'as pas une idée? Si

est une forme bilinéaire, comment pourrait-on la voir comme une application linéaire de E dans le dual de F?

par **barbu23** » 10 Mar 2010, 13:11

Nightmare a écrit:Tu n'as pas une idée? Si est une forme bilinéaire, comment pourrait-on la voir comme une application linéaire de E dans le dual de F?

Comme ça :

:happy3:

par **Nightmare** » 10 Mar 2010, 13:12

Je crois que c'est ça (je dis je crois car c'est pas vraiment compréhensible comme écriture :lol3: )

par **barbu23** » 10 Mar 2010, 13:14

Et quel est l'isomorphisme qui permet de dire que ces deux ensembles sont isomorphes :

?
:happy3:

par **Doraki** » 10 Mar 2010, 13:16

En disant que dans le truc de gauche, F est isomorphe à son dual ?

par **barbu23** » 10 Mar 2010, 13:22

barbu23 a écrit:Et quel est l'isomorphisme qui permet de dire que ces deux ensembles sont isomorphes : ?
:happy3:

Doraki a écrit:En disant que dans le truc de gauche, F est isomorphe à son dual ?

isomorphe à son dual ou bien à son bidual ? :happy3:

par **barbu23** » 10 Mar 2010, 13:25

??? :hein:

par **alavacommejetepousse** » 10 Mar 2010, 14:44

ils n ont pas la même dimension

par **alavacommejetepousse** » 10 Mar 2010, 14:45

Citation:
Posté par barbu23
Et quel est l'isomorphisme qui permet de dire que ces deux ensembles sont isomorphes : ?

ils n ont pas la même dimension

par **barbu23** » 10 Mar 2010, 14:46

D'accord, merci ! :happy3:

par **Doraki** » 10 Mar 2010, 14:56

Oui il faudrait remplacer tous tes produits cartésiens par des produits tensoriels.

par **barbu23** » 10 Mar 2010, 18:25

D'accord ! :happy3:
Sur le lien suivant, à la page : 8/9 :
http://www.imprimerie.polytechnique.fr/Cours/Files/Part3_Tome1.pdf
On parle de tenseurs mixtes d'ordre

de type

: c'est à dire, sous la forme :

telle que :

Et on dit que pour tout tenseur de ce type

, il existe un endomorphisme :

telle que :

Donc, c'est

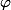
qui caracterise

de type

, et le differencie des autres tenseurs de même type :

Hier, dans une de mes questions sur un autre fil que personne ne m'y a pas repondu, est que les formes linéaires

sont des tenseurs de type

, telles que :

et on obtient :

A quoi correspond un tenseur

tel qu'il existe

tel que :

au lieu de ça :

comme on a vu tout à l'heure ?
MErci d'avance ! :happy3:

par **Ben314** » 10 Mar 2010, 18:37

Doraki t'a déjà répondu :

Doraki a écrit:Ils ne sont pas isomorphes, ils n'ont pas la même dimension.

par **barbu23** » 10 Mar 2010, 18:41

Ce truc là, me fait penser à l'ecriture de transposée d'un endomorphisme :
On voit souvent dans des bouquins des trucs comme ça :
Soit

un endomorphisme.
La formule suivant definit un unique endomorphisme :

tel que :

appelé transposée de

.
Et Donc,

:happy3:

Isomorphismes

Isomorphismes

Qui est en ligne