La "formule magique" est effectivement
trés utile (dans les cas ou elle s'applique...)
La preuve n'est franchement pas compliquée mais elle dépend de la façon dont on t'a défini les pôles et les résidus.
Le plus probable est que l'on t'ai défini les pôles comme les points
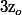
où la fonction f admet un développement en série de laurent, c'est à dire tels que :
=\sum_{n\geq -p}a_n h^n)
pour tout

assez petit.
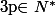
est appellé l'ordre du pôle (si on précise
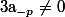
)
[Une définition équivalente consiste à dire qu'il existe
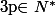
tel que la fonction
^pf(z))
se prolonge en une fonction holomorphe en
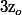
]
Le résidu de f en
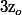
est alors le coefficient
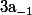
(i.e. celui en

).
Lorsque le pôle est d'ordre 1, le résidu est trés façile à calculer du fait que c'est lui qui donne l'équivalent de la fonction lorsque z tend vers
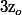
:
\sim_{0} =\frac{a_{-1}}{h})
donc
=a_{-1}=\lim_{h\rightarrow 0} hf(z_o+h))
(attention, ce n'est valable
que pour les pôles d'ordre 1 : pour un pôle d'ordre
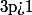
, on a
\sim_{0} =\frac{a_{-p}}{h^p})
qui ne permet bien sûr pas de calculer
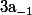
!).
Si

se présente sous la forme

où
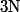
et
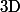
sont des fonctions holomorphes au voisinage de
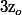
telle que
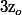
ne soit pas un zéro de
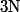
mais soit un zéro simple de
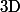
[c'est à dire
\not=0)
;
=0)
et
\not=0)
] alors
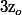
est un pole simple de

(évident) et on a :
\ =\ \lim_{h\rightarrow 0} h\,\frac{N(z_o+h)}{D(z_o+h)}\ <br />=\ \lim_{h\rightarrow 0} \frac{N(z_o+h)}{\big(D(z_o+h)-D(z_o)\big)/h}\ =\ \frac{N(z_o)}{D'(z_o)})
