Calcul d'intégral
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 03 Mar 2010, 15:47
par sky-mars » 03 Mar 2010, 15:47
Bonjour
Je souhaiterai calculer

en passant par le théorème des résidus... mon seul hic : le choix du contour
je voudrai avoir le moins de résidu à calculer mais apparemment c'est tendu !
J'avais penser à choisir un quart de cercle dans le plan (x,y) >0 en excluant x=1 en y mettant un petit cercle de rayon \epsilon mais bon je tombe sur un truc bizar....
qu'est ce que vous suggérez ? ? ?
merciiiiiiii
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 03 Mar 2010, 16:04
par MacManus » 03 Mar 2010, 16:04
Bonjour
Comme contour, tu peux prendre (dans le plan complexe) un rectangle défini de la façon suivante : la concaténation de 4 segments qui sont [-R,R], [R,R+iR], [R+iR, -R+iR] et [-R+iR, -R] avec R>1.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 03 Mar 2010, 16:09
par sky-mars » 03 Mar 2010, 16:09
hum mais avec ça j'aurai à me farcir tous résidus ...
La fonction est paire donc on peut restreindre l'étude sur
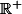
.
Peut être la moitié du contour pourra m'éviter la casse !
Tu connais le résultat de l'intégrale ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2010, 16:10
par Nightmare » 03 Mar 2010, 16:10
Salut !
Sinon, on peut prendre un contour formé des segments

et les arcs de cercles centré en 0 de rayon 1/n et n.
Il me semble que dans ce domaine, la fonction n'admet qu'un seul pôle. Par contre en faisant tendre n vers +oo on va trouver l'intégrale sur [0;+oo[ mais peu importe puisque la fonction qu'on intègre sur R tout entier a le bon goût d'être paire !
:happy3:
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 03 Mar 2010, 16:14
par MacManus » 03 Mar 2010, 16:14
je ne suis pas certain à 100% mais la valeur de l'intégrale est sans doute
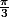
(à vérifier)
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 03 Mar 2010, 16:15
par sky-mars » 03 Mar 2010, 16:15
nightmare ton contour est tellement sophistiquée que j'arrive même pas à le visualiser :we: :we: :we: :ptdr: :marteau:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2010, 16:20
par Nightmare » 03 Mar 2010, 16:20
Je peux pas trop le faire à ta place mais il n'est pas très difficile à dessiner ! Qu'est-ce qui te gène?
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 03 Mar 2010, 16:20
par sky-mars » 03 Mar 2010, 16:20
la figure lol !
On a une genre de nappe ??
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2010, 16:22
par Nightmare » 03 Mar 2010, 16:22
avec des arcs de cercles? Ca risque d'être dur. Mon contour n'est pas plus difficile que celui de Macmanus.
Tu te fixes un n, tu traces le segment [1/n ; n] , le segment [1/n exp(i pi/3) ; n exp (i pi/3)] et tu relis leurs extrémités par les arcs de cercles.
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 03 Mar 2010, 16:33
par MacManus » 03 Mar 2010, 16:33
euh je n'ai sans doute pas tout saisi, pourquoi prendre
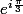
et non
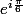
dans la définition du contour ??
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2010, 16:34
par Nightmare » 03 Mar 2010, 16:34
Ben, parce qu'avec exp(ipi/3) on a un unique pôle dans mon contour.

.
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 03 Mar 2010, 16:38
par MacManus » 03 Mar 2010, 16:38
d'accord merci Nightmare
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 03 Mar 2010, 16:53
par sky-mars » 03 Mar 2010, 16:53
c'est bon j'ai réussi à faire le calcul !
en fait comme un boulet dès le début j'avais tout faux sur mes pôles du coup j'ai pu prendre un contour sioux genre une portion de cercle partant de 0 à pi/3 assez ressemblant à nightmare sans les n ^^ avec un rayon R.
Le résultat qu'on trouve est
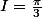

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Mar 2010, 19:31
par Ben314 » 03 Mar 2010, 19:31
Salut,
Pourquoi cherchez vous des contours aussi compliqué là ou le "classique" [-R,R] union le demi-cercle de centre (0,0) de rayon R marche trés bien ?
Si c'est pour "diminuer le nombres de pôles dans le domaine", il y a un truc qui m'échappe, les pôles c'est les z=exp((2k+1).pi/6) qui s'expriment à l'aide... d'une seule formule...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 03 Mar 2010, 19:33
par MacManus » 03 Mar 2010, 19:33
oui c'est ce que je pensais aussi pour l'expression des pôles... c'est pour ça que je posais la question à Nightmare (tu as oublié le "i" dans l'expression)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2010, 19:44
par Nightmare » 03 Mar 2010, 19:44
Pourquoi tout le monde trouve mon contour compliqué? En tout cas, il répond à la demande de Sky-Mars qui voulait un contour avec le moins de pôle possible.
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 04 Mar 2010, 03:07
par sky-mars » 04 Mar 2010, 03:07
Ben314 a écrit:Salut,
Pourquoi cherchez vous des contours aussi compliqué là ou le "classique" [-R,R] union le demi-cercle de centre (0,0) de rayon R marche trés bien ?
Si c'est pour "diminuer le nombres de pôles dans le domaine", il y a un truc qui m'échappe, les pôles c'est les z=exp((2k+1).pi/6) qui s'expriment à l'aide... d'une seule formule...
Salut,
c'était surtout pour éviter le calcul de résidus en prenant un contour avec le moins de pôles possible.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Mar 2010, 09:40
par Ben314 » 04 Mar 2010, 09:40
Si c'est pour "la beauté du geste", O.K. par contre si c'est le temps de calcul, je pense qu'on y perd à prendre un contours ne contenant pas [-R,R] du fait qu'il faut écrire l'intégrale sur la demi droite "non réelle" choisie et l'exprimer à l'aide de l'intégrale sur la demi droite réelle (bon, d'accord, ça prend une ligne...)
Alors que les résiduts et les poles, que tu en cherche 1 ou 6, c'est la même longueur :
Les pôles c'est les
i\pi}{6}\big)\ k\in\{0..5\})
(avec un 'i' !!!)
Et, vu que

et que les pôles sont racines simples de Q, les résidus sont les
}{Q'(z_k)}=\frac{z_k^2}{6z_k^5}= \frac{1}{6} z_k^{-3}=\frac{1}{6}\exp\big(-\frac{(2k+1)i\pi}{2}\big)=\frac{(-1)^{k+1}}{6}i\)
et je vois pas bien le gain de temps qu'on a à n'en calculer qu'un plutôt que les 6...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Black Jack
 par Black Jack » 04 Mar 2010, 15:07
par Black Jack » 04 Mar 2010, 15:07
Et sans passer par le théorème des résidus...
On pose x³ = t et on arrive au bout en 3 lignes.
:zen:
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 05 Mar 2010, 01:59
par sky-mars » 05 Mar 2010, 01:59
Bonsoir,
Pourquoi le résidu serait
}{Q'(z_k)})
? Je veux dire d'où viens cette formule :doh:
Pour moi sa aurait été un gain de temps par ce que je connaissais pas la formule magique que tu viens de me sortir en quelques secondes :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
