Paramètrage matriciel continu

par **Nightmare** » 26 Jan 2010, 18:18

Bonsoir !

Etant donné une fonction

qui à un vecteur de

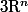
associe une matrice réelle carrée d'ordre n.

Si je suppose cette fonction continue et que M(t) a n valeurs propres, puis-je assurément construire un paramétrage continu des éléments propres?

Autrement dit, puis-je trouver deux fonctions

et

-respectivement à valeur dans

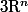
et

- continues et telles que

Bonne réflexion.

:happy3:

par **Ben314** » 26 Jan 2010, 18:27

De mémoire, la réponse est OUI, mais, même avec des conditions draconiènes sur la fonction t->M(t) on n'a jamais ne serait-ce que la dérivabilité des fonctions lambda_i(t) et des x_i(t)

P.S. Sauf si on suppose que les valeurs propres restent toujours distinctes sur l'intervalle, cas dans lequel tout coule de source...

par **Nightmare** » 26 Jan 2010, 18:30

Salut Ben314 !

Oui, c'est en fait un problème de raccord en gros et comme tu le dis, on peut raccorder continûment mais pas dérivativement.

par **barbu23** » 26 Jan 2010, 18:34

Nightmare a écrit:Bonsoir !

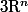
Etant donné une fonction qui à un vecteur de associe une matrice réelle carrée d'ordre n.

Si je suppose cette fonction continue et que M(t) a n valeurs propres, puis-je assurément construire un paramétrage continu des éléments propres?

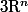
Autrement dit, puis-je trouver deux fonctions et -respectivement à valeur dans et - continues et telles que

Bonne réflexion.

:happy3:

Bonsoir : :happy3:
ça a l'air d'être comme ce qu'on voit en algèbre linéaire concernant les valeurs et vecteurs propres ! :happy3:
Souvent

doit être une application linéaire ! :happy3:

par **Ben314** » 26 Jan 2010, 18:42

barbu23 a écrit:ça a l'air d'être comme ce qu'on voit en algèbre linéaire concernant les valeurs et vecteurs propres ! :happy3

Je pense que oui, barbu, il y a de l'idée. :zen:

@Nightmare : Tu as une preuve assez simple ? Tu en cherche une ?
J'avais eu besoin d'un résultat équivalent ("suivre" les racines d'un polynôme dont les coeffs. dépendent continuement de t) il y a longtemps, et j'avais fini par trouvé un (vieux) article qui répondait à la question (et même beaucoup plus).
Sauf que j'ai (évidement) oublié les références et que de mémoire, ça coulait pas vraiment de source...

par **Doraki** » 26 Jan 2010, 18:42

En fait on suppose que M(t) est toujours diagonalisable et on doit montrer que M(t) est continûment diagonalisable ?

par **Nightmare** » 26 Jan 2010, 18:57

Ben314 > En fait l'idée de la preuve n'est pas difficile. Comme je te l'ai dit c'est un problème de "raccord". Localement, autour de 0, le théorème des fonctions implicites appliqué au polynôme caractéristique

de M(t) fournit un paramétrage continu au voisinage de 0 (bon en fait pas directement, mais ce n'est pas très dur de l'exhiber).

Tout ce qu'il reste à faire c'est le prolonger continûment à R (et non R^n comme le stipule mon énoncé erroné)

Doraki > Non on ne suppose pas M(t) seulement diagonalisable, on suppose en plus que son polynôme caractéristique scindé est à racines simples.

par **Ben314** » 26 Jan 2010, 19:05

Nightmare a écrit:Doraki > Non on ne suppose pas M(t) seulement diagonalisable, on suppose en plus que son polynôme caractéristique scindé est à racines simples.

Je comprend plus trop...

Si les racines du polynôme sont tout le temps distinctes, tu suit les racines par exemple à l'aide du Th. d'inversion locale, puis tu suit les vecteurs propres en disant que localement, leurs coordonnées se calculent à l'aide de sous determinants de la matrice.....

Pour moi, cela devient complexe lorsque l'on suppose que M(t) est diagonalisable pour tout t, mais que les sous espaces propres ne sont pas forcément de dim 1...

par **Doraki** » 26 Jan 2010, 19:12

Une fois qu'on a le théorème des fonctions implicites, ça ressemble plus à de la topologie algébrique qu'à de l'algèbre linéaire, nan ?

Je suis d'accord Ben, c'est plus rigolo de regarder des trucs comme
M(x,y) =
(x ; y)
(max(0,y); x)
Et de voir comment on est obligé de rajouter un bout de paramétrage pour pouvoir démêler tout le bazar ^^.

par **Nightmare** » 26 Jan 2010, 19:20

Ben314 a écrit:Je comprend plus trop...

Si les racines du polynôme sont tout le temps distinctes, tu suit les racines par exemple à l'aide du Th. d'inversion locale, puis tu suit les vecteurs propres en disant que localement, leurs coordonnées se calculent à l'aide de sous determinants de la matrice.....

Ben... c'était bien ça, j'ai jamais dit que le problème était difficile :lol3:

par **Ben314** » 26 Jan 2010, 20:07

Je suis en train de me poser une question con (étonant non).
La dernière fois que j'avais regardé la question, c'était dans C et, dans ce cas, il suffit de regarder les racines de

pour

pour voir qu'il y a peu d'espoir de les paramétrer de façon dérivable.
Mais un tel "contre-exemple" existe t'il dans R : coeff du polynôme trés réguliers (en t) et racines non dérivables (en t) ?

par **Doraki** » 26 Jan 2010, 20:16

Pt(X) = X^3-t ?

par **Ben314** » 26 Jan 2010, 21:43

Doraki a écrit:Pt(X) = X^3-t ?

...C'est pas faux...

D'ailleurs je me demande si le fameux "gros théorème" que j'avais vu ne disait pas justement que, si les coeffs du polynôme sont suffisement régulière (classe Ck ? Cinfini ? Analytique ? Polynômiales ?) alors on peut exprimer les racines du polynome de façon "régulières", pas en fonction de t, mais plutôt en fonction de t^(1/d) où d est le degrés du polynôme.

Edit : ton exemple me fait aussi penser que travailler dans C pour ce genre de problème, c'est quand même plus visuel : on voit mieux où est le problème lorsque l'on considère que X^3-t a 3 racines...

par **Ben314** » 26 Jan 2010, 22:47

Aprés, en supposant le paramétrage des racines du poly_car continues (je sais que c'est vrai mais je n'ais pas de preuve super simple), il reste la question d'une paramétrisation des vecteurs propres : est ce que ça ce "recolle" forcément a droite et à gauche d'un 't' pour lequel le poly_car a des racines multiples ???

Je pense que c'est à ça que tu pensait dans ton post #9...

par **Doraki** » 26 Jan 2010, 23:07

Ben dès que t'as des endroits où y'a des ensemble de vecteurs propres qui sont plus gros que des droites (genre M = Id), tu risques de devoir faire des sauts.

par **Ben314** » 26 Jan 2010, 23:41

Doraki a écrit:Ben dès que t'as des endroits où y'a des ensemble de vecteurs propres qui sont plus gros que des droites (genre M = Id), tu risques de devoir faire des sauts.

Est-ce si évident ??
Pour les deux malheureuse matrices 2x2 à paramètre que j'ai écrite on arrive à paramétrer continuement les vecteurs propres...
Evidement, c'est pas en regardant pile poil à l'endroit ou le s.e.v. et de dim>1 que tu saura quels sont les deux vecteurs que tu va choisir comme vecteurs propres, mais en regardant "un peu à coté".

Je me demande si on verrait pas mieux en "pur matriciel" : A(t) matrice dépendant continuement de t, diagonalisable pour tout t, donc il existe D(t) diagonale dépendant continuement de t (ça je sais que c'est vrai) qui est semblable à A(t) et, on cherche s'il est possible de trouver P(t) dépendant continuement de t telle que A(t)=P(t)D(t)P(t)^{-1}...

par **Doraki** » 27 Jan 2010, 00:03

Bah en partant de Id à t=0, tu peux faire un chemin sur des matrices ayant n'importe quel couple de vecteurs propres que tu veux.
Donc ça coince, suffit de mettre des couples de vecteurs propres différents avant et après Id.

Mais si tu t'autorises à paramétrer t par un paramètre p de manière à pouvoir arrêter le temps et recoudre les vecteurs propres pendant que t = 0 et M = Id...

par **Ben314** » 27 Jan 2010, 00:10

Doraki a écrit:Mais si tu t'autorises à paramétrer t par un paramètre p de manière à pouvoir arrêter le temps et recoudre les vecteurs propres pendant que t = 0 et M = Id...

Oui, mais je trouve que "mathématiquement parlant", ça n'a pas trop d'intérêt...

Doraki a écrit:Bah en partant de Id à t=0, tu peux faire un chemin sur des matrices ayant n'importe quel couple de vecteurs propres que tu veux.
Donc ça coince, suffit de mettre des couples de vecteurs propres différents avant et après Id.

Tu as (une fois de plus) raison, mais est-ce encore le cas si on suppose que t->A(t) est dérivable (voir de classe C1) ?

[Evidement, je dit ça du fait que je n'ais essayé que des t->A(t) polynômiales...]

par **Doraki** » 27 Jan 2010, 00:13

Ah ben là j'ai plus d'argument pour penser que ça marche plus.

par **Ben314** » 27 Jan 2010, 00:15

Doraki a écrit:Ah ben là j'ai plus d'argument pour penser que ça marche plus.

ahhhh, quand même !!!!! :zen:

Paramètrage matriciel continu

Paramètrage matriciel continu

Qui est en ligne