Parametrage curviligne[48h]

[fourize]

bonsoir !

la bête des 48 heures qui suivent est la suivante:

considérons la courbe est parametré par abscisse curviligne. on note L la plus petite période de (L est d'ailleurs la longueurs de la courbe ) on fait les hypothèses suivantes :
* est injective sur [0,L[.
* la courbe est convexe.
1. justifier que est L periodique .
2. on considere la courbe T(s) = (x'(s),y'(s)). T est de classe C² . en calculant la norme de T(s) en tout s, definir et dessiner la trace de

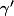
l'énoncé est bien compréhensible ce qui me pose probleme ce que je n'ai rien de plus sur x(s) et y(s), et je ne vois pas quelque chose de théorique à utiliser pour mes deux questions ?

toute proposition sera donc la bienvenue et merci d'avance de votre lecture.

[MacManus]

Bonjour

Pour la 1) je ne suis pas sûr si ce que je vais dire est correct, mais peut-être faut-il revenir à la définition même de la longeur d'un arc parcouru durant une période L à une vitesse curviligne égale à à l'instant s, soit : Je dis peut-être une grosse c****rie..., mais bon puisque tte proposition est la bienvenue. (Normalement la longueur d'un arc géométrique fait intervenir la dérivée et la norme)

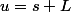
En écrivant et en effectuant le changement de variable , on obtient que =, et comme est injective, c'est égal à

Mais on peut sans doute utiliser les coordonnées (x(s),y(s)) ou les coordonnées polaires... Bref ma réponse me semble bien naïve.

[fourize]

je suis juste de passage devant un ordi !
donc pas le temps de réflechir à ta reponse MacManus ! mais j'y verrai cette après midi !
par contre moi on m a appris que la longueur d'une courbe (parametré ) est :
Long =

encore une idée ... ?

PS. MacManus, la vitesse parcouru par une courbe à l'instant s n'est pas mais plutôt

[MacManus]

oui je suis d'accord, moi aussi on me l'a appris comme ça
J'ai vu ça sur wikipédia, mais bon...je trouvais ça étrange aussi. Il y avait la définition que ns connaissons, puis cette formule aussi, je ne sais pas pourquoi...http://fr.wikipedia.org/wiki/Longueur_d'un_arc(partie 2.1)