Barycentre.

par **lolotte83** » 13 Déc 2009, 11:53

Bonjour, j'ai des difficultés en mathématiques, et particulièrement sur les barycentres, mon professeur ma donné un devoir maison concernant "Associativité" et "Ensemble des points".
En voici l'énoncé :
Exercice 1:
ABC étant un triangle quelconque,
On appelle I le symétrique de B par rapport a C, J vérifie la relation AJ = 2/5 AC
et K est le symétrique du milieu du segment [AB] par rapport a A.
1) Faire une figure ( fait )
2) Exprimer les points I, J et K en tant que barycentre des points A,B et C. ( J'aimerai une explication de ce qui y est demandé svp )
3) Montrer que les droites (AI) et (BJ) se coupent au milieu du segment [KC].

Exercice 2:
ABCD est un carré de centre O et de coté 4cm.
G est le barycentre du système pondéré {(B;1);(C;-4);(D;1)}
1)Montrer que pour tout point M du plan,
MA - MB + MC -MD = 2AB
2) Montrer que G est le symétrique de O par rapport a C.
3) Déterminer et construire l'ensemble des points M du plan tels que :
|| MB - 4MC + MD || = || MA - MB + MC - MD ||

J'aimerai des indications ou des méthodes pour le réussir, merci d'avance. :help:

par **Dr Neurone** » 13 Déc 2009, 11:59

Bonjour lolotte 83

par **Ben314** » 13 Déc 2009, 12:37

Bonjour,
Pour le 2) on te demande de trouver des réels ? tels que I soit le barycentre de (A,?), (B,?) et (C,?). Idem pour J et K.
Pour celà, il te faut "traduire" en terme de barycentre les phrases :
a) I est le symétrique de B par rapport a C
b) J vérifie la relation

c) K est le symétrique du milieu du segment [AB] par rapport a A.
Dans chaque cas, il faut que tu trouve une égalitée vectorielle pour traduire la phrase (pour le b), il n'y a rien à faire...) puis que te te débrouille pour transformer cette égalité en une égalité du type

(si c'est I que tu cherche à écrire comme barycentre).
Ce n'est pas trés compliqué est assez mécanique...

Bon courage

par **lolotte83** » 13 Déc 2009, 12:47

Merci beaucoup pour cette explication ! :we:
Peux-tu me donner une indication qui me permettrais de demarrer le 1) de l'exercice 2 ?

par **Ben314** » 13 Déc 2009, 12:59

Pour "simplifier" une expression du type

qui contient 4 fois la lettre M (qui est l'"inconnue" de la formule : les autres points sont connus) on se dit que pour les "regrouper" il faudrait que tous soit de la même forme

pour un certain point X et on peut se rammener à cela en "coupant" par exemple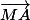

en

Souvent le "meilleur" point X est le barycentre de A,B,C,D affecté des coeff qui aparaissent devant les vecteurs, mais ici on ne peut pas car 1+(-1)+1+(-1)=0 donc le barycentre n'existe pas.
On prend donc pour X un point quelconque, par exemple le point A ou le point B (tu peut aussi prendre un point 'X' quelconque puis, plus tard dans les calculs, te rendre compte que ca simplifierais bien avec tel point X bien particulier...)

par **Dinozzo13** » 13 Déc 2009, 13:01

Exercice 1 :
2°)Ici, il me semble que tu dois exprimer I,J et K en fonction de A,B et C.
je te montre pour le 1er : I est milieu de [BC] donc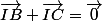

et par conséquent, I le barycentre de (A,0),(B,1),(C,1). A toi de faire les deux autres.
3) Il y a un pblm soit dans ta question, soit dans l'énoncé.

Exercice 2 :
il y a plusieurs étapes :
- Exprime le barycentr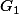e

de

.
- Pour

reporte toi au 1°) de cet exo
- M appartient à cet ensemble si et seulement si

- Tu en déduis donc l'ensemble des points M.

par **lolotte83** » 13 Déc 2009, 13:34

Merci beaucoup a vous deux, sauf que pour le 3) de l'exercice 1, AI et BJ se coupent bien au milieu de KC, j'ai fais une figure GeoGebra.

par **lolotte83** » 13 Déc 2009, 13:46

Mon professeur m'a envoyer un mail comme quoi il y a presence d'une erreur dans le devoir, dans l'exercice 2 : " remplacer: MA - MB + MC - MD = 2 AB par: MB - MA + MC - MD = 2 AB "
Est ce que cela change quelque chose ??
Merci de m'aider !

par **Ben314** » 13 Déc 2009, 13:51

Concernant la méthode, cela ne change absolument rien (car la somme des coeffs. vaut toujours 0)...
Par contre, concernant le résultat que tu vas trouver, ça change les choses !!!

par **lolotte83** » 13 Déc 2009, 14:07

"Souvent le "meilleur" point X est le barycentre de A,B,C,D affecté des coeff qui aparaissent devant les vecteurs, mais ici on ne peut pas car 1+(-1)+1+(-1)=0 donc le barycentre n'existe pas.
On prend donc pour X un point quelconque, par exemple le point A ou le point B (tu peut aussi prendre un point 'X' quelconque puis, plus tard dans les calculs, te rendre compte que ca simplifierais bien avec tel point X bien particulier...)"
Je ne comprend pas trop l'histoire du X ...
J'ai commencé comme cela : MB - MA + MC - MD =2AB
MO+OB-MO-OA+MO+OC-MO-OC=2AB
OB-OA+OC-OD=2AB , ce qui me parait faut car O est le barycentre de ABCD ... Je suis perdu :S

par **Ben314** » 13 Déc 2009, 14:30

Dans ce genre d'exo., il vaut mieux éviter d'écrire directement le résultat que l'on te demande de montrer (tu ne cherche pas les M pour lesquels ça marche, tu veut montrer que ca marche pour tout le M...)
Donc je te conseillerait plutot d'écrire :
MB - MA + MC - MD = MO+OB-MO-OA+MO+OC-MO-OC
= OB-OA+OC-OD = ... = 2AB
Ici, tu doit compléter les ... (ce qui n'est pas dur du tout en (re) regroupant les vecteurs)
Par contre d'avoir introduit le point O dans les calculs n'est pas trés astucieux : le résultat final que tu doit trouver ne contient pas la lettre O.

Une fois que tu aura complété les ... ci dessus, essaye de réécrire la même chose en introduisant le point A à la place de O : tu verra que c'est (un peu) plus simple.

par **lolotte83** » 13 Déc 2009, 14:36

J'ai complété les "..." en introduisant A dans OB-OA+OC-OD=2AB, est ce juste ou doit-je quand même faire :
MA + AB - MA + MA + AC - MA - AD = 2 AB
AB + AC - AD = 2AB
AC - AD = AB ?

par **Ben314** » 13 Déc 2009, 14:39

Il te suffit (évidement) de faire un seul des deux, donc soit tu as déjà écrit "au propre" avec O et tu laisse comme ça, soit tu n'as pas encore écrit "au propre" et tu prend plutôt l'autre méthode qui est plus courte.

par **lolotte83** » 13 Déc 2009, 14:51

Grand merci pour toutes tes explications, mais je ne vois pas trop en quoi cela a un rapport avec tout les point M du plan, quel est le rapport avec AC - AD = AB et M ? :S

par **Ben314** » 13 Déc 2009, 15:03

Bon, je te donne la rédaction telle que je la ferais :

MB - MA + MC - MD = (MA+AB) - MA + (MA+AC) - (MA+AD)
= MA+AB-MA+MA+AC-MA-AD = AB+AC-AD (les MA s'éliminent)
= AB + AC + DA (car -AD=DA)
= AB + DC (car DA+AC=DC)
= AB + AB (car ABCD est un carré donc DC=AB )
=2AB

par **lolotte83** » 13 Déc 2009, 15:24

:++: Encore merciiiii !!!! :we: :we: :we: :we: :we:

Barycentre.

Barycentre.

Qui est en ligne