Sommes vectorielles et lieux géométriques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Toni2
- Membre Relatif
- Messages: 185
- Enregistré le: 13 Sep 2009, 18:50
-
 par Toni2 » 04 Nov 2009, 21:10
par Toni2 » 04 Nov 2009, 21:10
Et bien pour moi

puisque 1+(-1)=0... mais apparemment non !
Mais il faut donc changer l'expression alors puisqu'il n'a pas de barycentre , faut-il que j'introduise un point dans cette expression ? Je voi que cette solution =S non?
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 04 Nov 2009, 21:22
par zerkel » 04 Nov 2009, 21:22
NON ta propriété n'est justement vraie que si la somme des coefficients est non nulle!
REMPLACE LE

par
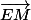
dans ton expression et regarde la droit dans les yeux... Ne serait_ce pas la forme développée d'un vecteur après avoir utilisé la relation de Chasles?
-
Toni2
- Membre Relatif
- Messages: 185
- Enregistré le: 13 Sep 2009, 18:50
-
 par Toni2 » 04 Nov 2009, 21:32
par Toni2 » 04 Nov 2009, 21:32
Si,

équivaut à

Alors forme développer du vecteur

-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 04 Nov 2009, 21:35
par zerkel » 04 Nov 2009, 21:35
voilà! Maintenant tu retournes à ta relation sur les normes et tu conclus!
-
Toni2
- Membre Relatif
- Messages: 185
- Enregistré le: 13 Sep 2009, 18:50
-
 par Toni2 » 04 Nov 2009, 21:38
par Toni2 » 04 Nov 2009, 21:38
Et oui mon dieux..

donc l'ensemble (r) des points M
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 04 Nov 2009, 21:42
par zerkel » 04 Nov 2009, 21:42
Tu devrais avoir une égalité de NORMES avec le point M dedans, sinon c'est un peu dur de trouver le lieu des points M :p
-
Toni2
- Membre Relatif
- Messages: 185
- Enregistré le: 13 Sep 2009, 18:50
-
 par Toni2 » 04 Nov 2009, 21:46
par Toni2 » 04 Nov 2009, 21:46
-_- oui c'est vraie....

-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 04 Nov 2009, 21:47
par zerkel » 04 Nov 2009, 21:47
Donc le lieu des points M qui vérifient cette relation est...
-
Toni2
- Membre Relatif
- Messages: 185
- Enregistré le: 13 Sep 2009, 18:50
-
 par Toni2 » 04 Nov 2009, 21:52
par Toni2 » 04 Nov 2009, 21:52
Oui ça aussi sa serait bien je le dise ^^
Donc, L'ensemble (r) des points M sont : Le cercle C de centre G2 et de rayon

-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 04 Nov 2009, 21:57
par zerkel » 04 Nov 2009, 21:57
Oui, mais n'oublie pas de mettre la norme pour la valeur du rayon ça ferait tâche sur la copie ;).
-
Toni2
- Membre Relatif
- Messages: 185
- Enregistré le: 13 Sep 2009, 18:50
-
 par Toni2 » 04 Nov 2009, 21:58
par Toni2 » 04 Nov 2009, 21:58
^^ Je te remercie encore une fois énormément, je n'aurais vraiment pas fait long feu si tu ne m'aurais pas aidé ! Bonne soirée =) !
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Nov 2009, 22:13
par Dinozzo13 » 04 Nov 2009, 22:13
Je te propose une petite correction du 1°) au cas où :
Soit
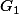
l'isobarycentre de

,

et

, on a, d'après la propriété fondamentale, pour tout point

du plan :

.
Soit
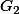
le barycentre de
)
,
)
, on a, d'après la propriété fondamantale, pour tout point

du plan :

.

si et seulement si

, c'est-à-dire,
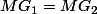
.

est la médiatrice de
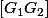
.
Par définition,
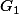
est l'isobarycentre de

,

et

, donc :

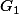
est donc le centre de gravité du triangle

.
Par définition,
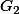
est le barycentre de
)
,
)
, donc :





.
Voilà :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 157 invités
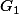 l'isobarycentre de
l'isobarycentre de  ,
, et
et  , on a, d'après la propriété fondamentale, pour tout point
, on a, d'après la propriété fondamentale, pour tout point  du plan :
du plan : .
.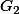 le barycentre de
le barycentre de ) ,
,) , on a, d'après la propriété fondamantale, pour tout point
, on a, d'après la propriété fondamantale, pour tout point  du plan :
du plan : .
. si et seulement si
si et seulement si  , c'est-à-dire,
, c'est-à-dire, 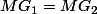 .
. est la médiatrice de
est la médiatrice de 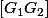 .
.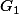 est l'isobarycentre de
est l'isobarycentre de  ,
, et
et  , donc :
, donc :
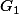 est donc le centre de gravité du triangle
est donc le centre de gravité du triangle  .
.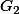 est le barycentre de
est le barycentre de ) ,
,) , donc :
, donc :



 .
.