Barycentre: sommes vectorielles

[Anonyme]

ABC est un triangle. G est son centre de gravité et K le barycentre de (A,2) , (B,2) , (C,-1).
Déterminer, puis construire l'ensemble des points M du plan tels que:
a)2MA*+2MB*-MC* soit colinéaire à BC*
b)||2MA*+2MB*-MC*||= ||2MA*-MB*-MC*||
c)||2MA*+2MB*-MC*||=||MA*+MB*+MC*||

(*=vecteur)

svp aider moi , c'est urgent! merci beaucoup

[becirj]

Bonjour

Il faut réduire les différentes sommes.

Dans le vecteur , il faut introduire le barycentre K de (A,2), (B,2) , (c,-1).

Dans le vecteur , il faut introduire le centre de gravité du triangle.

est un vecteur constant, indépendant de M, que tu peut exprimer en fonction de 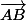et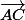

De manière générale, pour réduire de telles sommes, si la somme des coefficients est non nulle on introduit le barycentre, si elle est nulle il s'agit d'un vecteur indépendant de M