Questions de cours : équations ax+by=c

par **Dinozzo13** » 03 Nov 2009, 13:48

:ptdr: , licence, voire même prépa ^^

par **benekire2** » 03 Nov 2009, 13:51

Dinozzo13 a écrit::ptdr: , licence, voire même prépa ^^

Purquoi voire même, la prépa MPSI puis MP c'est le même niveau en math que L1 L2 Math, c'est pas inférieur ( sauf sur le programme de PC)

par **Dinozzo13** » 03 Nov 2009, 13:58

J'aimerai confirmer mes acquis, pourrais-tu me dire si c'est juste, merci ^^.
Je veux résoudre dans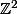

: 1041x+241y=62
Soit d=PGCD(1041,241), d'après l'algorithme d'Euclide :
1041=4x241+80
241=80x3+1
80=1x80
1041 et 241 sont premiers entre eux donc d divise 62.
Je cherche une solution particulière

en remontant l'algorithme d'Euclide :
1=241-80x4
1=241-(1041-4x241)x4=241-4x1041+16x241=-4x1041+17x241
Donc une solution particulière est

.
Par conséquent

est-ce que écrire dans cet exo d=PGCD(x,y) c'est pareil que d'écrire

?
Quand je dis 1041 et 241 sont premiers entre eux donc d divise 62, est-ce que c'est la même chose quand je dis que d=1 donc d|62 ?

par **Dinozzo13** » 03 Nov 2009, 14:04

benekire2 a écrit:Purquoi voire même, la prépa MPSI puis MP c'est le même niveau en math que L1 L2 Math, c'est pas inférieur ( sauf sur le programme de PC)

wai, la différence c'est qu'on a quasiment pas de temps libre en prépa.

par **benekire2** » 03 Nov 2009, 14:05

ta résolution me semble tout a fait juste, après pour ta question sur la division oui c'est pareil masi pour le pgcd, je ne sais pas, pour moi ce signe veut dire "et" donc a la limite tu met max(d)|x"et"y <=> PGCD(x,y) ce qui est plus simple selon moi

par **Dinozzo13** » 03 Nov 2009, 14:10

j'vais en refaire une dizaine à faire pour voir si j'ai tout pigé, tu pourras voir si elles sont justes, merci ^^.

par **Dinozzo13** » 03 Nov 2009, 14:42

j'ai un doute, quand on dis que a|b, ça veut bien dire que le reste de la division de a par b est nul, autrement dis,

par **benekire2** » 03 Nov 2009, 15:01

Oui de toute façon en terminale, les congruence ne sont q'un autre moyen de traduire les relations de la division euclidienne, mais oui tout ce que tu as dit est équivalent!!
Vas y je vérifierais ( je te promet pas d'être parfait, je n'ai jamais fait d'équations diophantiennes , enfin j'y arrive, parce que j'ai pas fini totalement le prog de spé)

par **benekire2** » 03 Nov 2009, 15:03

Concernant la prépa, oui c'est sur!! Mais si tu bosses tout seul correctement à la fac, tu n'as pas beaucoup de temps non plus!

par **Dinozzo13** » 03 Nov 2009, 21:39

On a vu précédement que

dans

avait pour solution

. Comment aurais-t-on fait s'il fallait résoudre dans

?

par **Le_chat** » 03 Nov 2009, 21:45

Tu as faux quelque part, a vu de nez. Les "k" dans les solutions doivent s'annuler, ici tous les coefs devant les k sont positifs, comme les coefs de l'equation diophantienne.

par **Dinozzo13** » 03 Nov 2009, 21:47

Non, je voulais dire

.

par **Le_chat** » 03 Nov 2009, 21:52

Dinozzo13 a écrit:Non, je voulais dire .

La c'est bon...

par **Dinozzo13** » 03 Nov 2009, 21:56

erreur de frappe :ptdr:
Mais je me suis demandé comment on l'aurait résolue dans

.

par **Dinozzo13** » 03 Nov 2009, 22:06

Ca ne se résous peut-être pas dans cet ensemble ?

par **Le_chat** » 03 Nov 2009, 22:11

Heu Zi c'est les imaginaires purs?

par **Nightmare** » 03 Nov 2009, 22:14

Dinozzo13 a écrit:A propos des congruences, résoudre c'est résoudre
ax + by = 1, non ?
Pourrais-tu m'expliquer ce paragraphe :
La résolution de l'équation ax + by = 1, où a et b sont premiers entre eux, permet de trouver un inverse à a modulo b, c'est-à-dire un entier x tel que .L'ensemble des solutions permet de dire qu'il existe une unique classe x tel que ax=1 dans . En effet, parmi les couples solutions, tous les entiers x sont congrus modulo b.

Salut,

tu sais que dans R, l'inverse d'un nombre x est 1/x. En fait plus généralement, dans un "ensemble" quelconque (en fait il faut un ensemble et une opération) l'inverse d'un élément x est un élément y tel que x*y=1 (On a bien x * 1/x = 1 dans R).

Z/pZ est grossièrement l'ensemble des restes dans la division par p. En fait dans Z/pZ on a pas des nombres mais des classes de nombre, chaque classe représentant tous les nombres qui ont le même reste dans la division par p. Ainsi, par exemple dans Z/11Z , 1, 12, 23, 34 etc.. ont le même reste dans la division par 11 ( égal à 1) et font partie de la même classe qu'on va noter

. Bref, au lieu de compter 0,1,2,3,...,11,12,13,14,.... c'est comme si on comptait 0,1,2,3....,9,10,0,1,2,3....,.

Bref, tout ça pour dire que comme dans R, on peut définir une inverse pour la multiplication, c'est à dire que pour nombre donné x, on peut chercher un élément y tel que xy=1 (modulo p), le nombre y étant appelé inverse. Tu démontreras que cette inverse existe si et ssi x et p sont premiers entre eux (Que dire du coup si p est premier?)

En espérant être compréhensible.

:happy3:

par **Dinozzo13** » 03 Nov 2009, 22:19

Assez, merci ^^.

Le_chat a écrit:Heu Zi c'est les imaginaires purs?

par **Le_chat** » 03 Nov 2009, 22:48

Dinozzo13 a écrit:

J'ai jamais fait sa, mais sa doit etre pareil que dans Z, avec deux equa diophantiennes a résoudre, en identifiant les parties imaginaires et réelles

par **Dinozzo13** » 04 Nov 2009, 22:18

comment cela ??? :doh:

Questions de cours : équations ax+by=c

Qui est en ligne