Continuité par image inverse des ouverts

[ElVinze]

Bonjour! Va relire le réglement et respecte le!

Voici un texte que j'ai trouvé sur un autre forum :


En topologie, on peut se donner une collection de sous ensembles d'un ensemble X vérifiant certains axiomes. C'est ce qu'on appelle une topologie T.
Dans R^n, tu peux montrer qu'une fonction f de X vers Y vérifie que
f^(-1)(ouvert de Y)=ouvert de X
si et seulement si f est continue (idem avec les fermés)
Si on en revient à notre espace topologique, on ne peut plus définir la continuité par des limites ou des epsilon et des lambda, puisque la seule chose que l'on connait sur notre espace topologique, est "quels sont les ouverts, et fermés"
Avec la remarque ci-dessus, on va définir la continuité de la même façon.
Notamment, si je prend R muni de la topologie discrete, Y=(R,Tdiscrete) et que je prend R munie de la topologie usuelle (la topologie engendrée par la valeur absolue) X=(R,Tusuelle)
Alors dans ce cas, ta fonction x^2 n'est pas continue, et c'est même très facile à montrer.

Donc j'essaie de montrer que x^2 n'est pas continue dans ce contexte et je n'y arrive pas ...

[mathelot]

bonsoir,

Un point est ouvert dans la topologie discrète

exemple: est habituellement muni de la topologie
discrète car


donc si Y est muni de la topologie discrète, un nombre(c'est à dire un point)
est un ouvert, son image réciproque par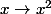 est une paire. Ce sous-ensemble de R n'est pas un ouvert pour la topologie habituelle. la fonction "élever au carré" n'est pas continue.

[ElVinze]

Ça a le mérite d'être super simple à montrer ... mais une autre question me vient en tête, est-ce qu'il existe des fonctions continues qui vont de l'espace métrique (R,usuelle) vers (R,discrete)?

[Finrod]

Les fonctions constantes par morceaux, aussi appelées fonctions en escalier.

[ffpower]

euh,non,que les fonctions constantes,R étant connexe(c est meme la définition de connexité)

[Finrod]

Ah oui tiens pardon. *Part se cacher

ce qui tend à montrer que cela s'interprète bien intuitivement (ouf) , les fonctions constantes étant résolument continues.

[ElVinze]

mmm alors il me semblait bien aussi ...