Convergence d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 03 Oct 2009, 19:01
par lapras » 03 Oct 2009, 19:01
Bonsoir,
j'ai une suite

qui vérifie :
u_{n-1})
avec

fixé.
j'aimerais montrer que

a une limite (finie ou infinie).
Auriez vous des indications ?
Lapras

-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 03 Oct 2009, 19:25
par Zavonen » 03 Oct 2009, 19:25
Si v_n=u_n+1-u_n
On a:
|v_n|<=(1-a)|v_n-1
Donc la série de terme général v_n est absolument convergente d'après le critère de d'Alembert.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 04 Oct 2009, 06:53
par lapras » 04 Oct 2009, 06:53
j'avais essayé ca mais je ne suis pas d'accord :
on a v_{n+1} <= -(1-a)V_{n}
mais on ne peut pas passer aux valeurs absolues !
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 04 Oct 2009, 07:00
par Zavonen » 04 Oct 2009, 07:00
mais on ne peut pas passer aux valeurs absolues !
Exact!, désolé...
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 04 Oct 2009, 08:01
par Zavonen » 04 Oct 2009, 08:01
J'ai l'impression que le cas a quelconque n'est pas différent du cas a=1/2.
Bornons nous pour le moment à étudier ce cas particulier.
Soit d=|u1-u0|
Une suite telle que tu proposes a à chaque 'instant' n une possibilité de croissance 'instantanée' de d/2^n et de croissance 'globale' majorée par d/2^(n-1).
La limite inférieure de la suite existe toujours dans la droite réelle achevée et elle est soit -infini soit une valeur finie.
Il me semble que la remarque ci-dessus doit permettre d'assurer que si la lim inf est finie la suite est convergente et sinon elle tend vers -infini. Je ne l'ai pas formalisé.
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 04 Oct 2009, 16:43
par wserdx » 04 Oct 2009, 16:43
Je pense que la condition implique
)
La suite
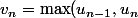)
est donc décroissante
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités