TS : Intro à la fonction exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2009, 18:24
par girdav » 16 Sep 2009, 18:24
magnum13 a écrit:}(x))'=(-1)^{n} (e^{-x} + ((x-n) (-e^{-x})) <br />= (-1)^{n} (e^{-x} (n-x+1))
Attention! Le - a disparu. Maintenant ça devrait être ok.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 16 Sep 2009, 19:35
par magnum13 » 16 Sep 2009, 19:35
}(x))'=(-1)^{n} (e^{-x} + ((x-n) (-e^{x})) <br />= (-1)^{n} (e^{-x} (x-n-1))
Mais après, ma démonstration est finie ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2009, 19:40
par girdav » 16 Sep 2009, 19:40
Il faut factoriser par

pour obtenir la bonne forme.
Tu as démontré que la propriété est vraie au rang initial et que si elle est vraie à un rang elle le sera au suivant.
La démonstration est donc finie.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 16 Sep 2009, 19:42
par magnum13 » 16 Sep 2009, 19:42
girdav a écrit:Il faut factoriser par

pour obtenir la bonne forme.
Tu as démontré que la propriété est vraie au rang initial et que si elle est vraie à un rang elle le sera au suivant.
La démonstration est donc finie.
Factoriser par -1, je vois pas, désolé mais la factorisation, c'est pas mon truc
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2009, 19:48
par girdav » 16 Sep 2009, 19:48
Il te faut un
^{n+1})
devant. Ce n'est rien d'autre que
^n)
Tu peux faire apparaître le moins qu'il faut en écrivant
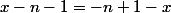)
.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 17 Sep 2009, 16:54
par magnum13 » 17 Sep 2009, 16:54
Alors, je pense avoir trouvé, voila ma rédaction :
Initialisation :
 = e^{-x} + x . (-e^{-x}) = e^{-x}(1-x))
Donc P(1) est possible.
Hérédité :
}(x))'=(-1)^{n} (-e^{-x})(x-n)+e^{-x}=(-1)^{n+1}.(e^{-x}.x-n+e^{-x})=(-1)^{n+1}.(e^{-x}).(x-n+1))
C'est bon ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Sep 2009, 17:57
par girdav » 17 Sep 2009, 17:57
P(1) est
vrai et non "possible".
Sinon je crois qu'il y a des erreurs (de calcul) dans la preuve de l'hérédité: après le premier égal
^n)
est facteur de "tout le truc", dans lequel on a
e^{-x} -e^{-x})
, ensuite après le deuxième signe égal tu as
^{n+1}\(e^{-x}\(n-x\)+e^{-x}\))
(erreur de factorisation). Maintenant ça devrait être bon.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 17 Sep 2009, 18:00
par magnum13 » 17 Sep 2009, 18:00
girdav a écrit:P(1) est
vrai et non "possible".
Sinon je crois qu'il y a des erreurs (de calcul) dans la preuve de l'hérédité: après le premier égal
^n)
est facteur de "tout le truc", dans lequel on a
e^{-x} -e^{-x})
, ensuite après le deuxième signe égal tu as
^{n+1}\(e^{-x}\(n-x\)+e^{-x}\))
(erreur de factorisation). Maintenant ça devrait être bon.
Pourrai tu m'expliquer mieux mes erreurs, je ne comprends pas !
Merci
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Sep 2009, 18:05
par girdav » 17 Sep 2009, 18:05
En gros il y a des erreurs de factorisation.
^n)
est considéré comme une constante, donc il doit être mis en facteur de la dérivée du "reste" de
})
.
Pose
 = n-x)
et
 = e^{-x})
.
On a
 =-1)
et
 = -e^{-x})
donc la dérivée de
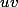
est
e^{-x})
. Factorise par

et ça devrait être bon (en faisant le lien avec
})
).
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 17 Sep 2009, 19:42
par magnum13 » 17 Sep 2009, 19:42
Mais ça c'est bien bon non ?
}(x))'=(-1)^{n} (-e^{-x})(x-n)+e^{-x})
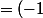^{n+1}.(e^{-x}.x-n+e^{-x}))
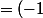^{n+1}.(e^{-x}).(x-n+1))
La première ligne, je dérive
}(x))
La deuxième ligne, j'ajoute le -1 du
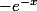
Et pour finir, je met en facteur

et j'ai bien ce que je recherche.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Sep 2009, 19:47
par girdav » 17 Sep 2009, 19:47
C'est
^{n+1}e^{-x}\(n+1-x\))
que tu dois trouver.
Tu as oublié un moins devant le deuxième

de la deuxième ligne.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 19 Sep 2009, 17:02
par magnum13 » 19 Sep 2009, 17:02
girdav a écrit:C'est
^{n+1}e^{-x}\(n+1-x\))
que tu dois trouver.
Tu as oublié un moins devant le deuxième

de la deuxième ligne.
Non, c'est
^{n+1}e^{-x}\(x-n+1\))
que l'on doit trouver puisque dans la fonction
}(x))
on a (x-n) et non (n-x)
Non ?
Merci
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 19 Sep 2009, 18:27
par magnum13 » 19 Sep 2009, 18:27
S'il vous plait c'est pour lundi !!
Merci
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 19 Sep 2009, 20:00
par girdav » 19 Sep 2009, 20:00
Je me suis trompé. Pour me faire pardonner:
On a
^n\(x-n\)e^{-x}}{\partial x}=\partial \(-1\)^n\fr{\(x-n\)e^{-x}}{\partial x} = \(-1\)^n\[1.e^{-x}+\(x-n\).(-1)e^{-x}\]<br />=\(-1\)^ne^{-x} \[1-\(x-n\)\])
et tu devrais pouvoir conclure.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 19 Sep 2009, 21:01
par magnum13 » 19 Sep 2009, 21:01
girdav a écrit:Je me suis trompé. Pour me faire pardonner:
On a
^n\(x-n\)e^{-x}}{\partial x}=\partial \(-1\)^n\fr{\(x-n\)e^{-x}}{\partial x} = \(-1\)^n\[1.e^{-x}+\(x-n\).(-1)e^{-x}\]<br />=\(-1\)^ne^{-x} \[1-\(x-n\)\])
et tu devrais pouvoir conclure.
Je ne comprends pas la dernière égalité avec le (1-(x-n)) Pourquoi +1 ce n'est pas le "-" du
)
?
Je ne comprends pas
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 19 Sep 2009, 21:04
par girdav » 19 Sep 2009, 21:04
Après tu peux écrire
 = -\(x-n-1\)=-\(x-\(n+1\)\))
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 19 Sep 2009, 21:08
par magnum13 » 19 Sep 2009, 21:08
girdav a écrit:Après tu peux écrire
 = -\(x-n-1\)=-\(x-\(n+1\)\))
A ok donc ça fait
^n . (e^{-x}).(-1).(x-(n+1)))
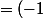^{n+1} . (e^{-x}).(x-(n+1)))
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 20 Sep 2009, 08:11
par girdav » 20 Sep 2009, 08:11
C'est ça! Tu n'as plus qu'à recoller les morceaux pour demain.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 20 Sep 2009, 09:35
par magnum13 » 20 Sep 2009, 09:35
girdav a écrit:C'est ça! Tu n'as plus qu'à recoller les morceaux pour demain.
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
est facteur de "tout le truc", dans lequel on a
, ensuite après le deuxième signe égal tu as
(erreur de factorisation). Maintenant ça devrait être bon.