équation

[ditans]

bonjour, je dois démontrer que l'équation suivante admet une seule solution qu'on note



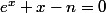
Il faut utiliser le théoreme des valeurs intermediares? Et donc montrer qu'elle est monotone ? J'ai aucune idee ...
merci!

[zerroudi]

oui tu peux utiliser le théoreme des valeurs intermediares :
Soient f et g deux fonctions continues sur un intervalle non vide [a ; b] de R, telles que g(a) - f(a) et g(b) - f(b) soient de signes contraires. Il existe au moins un réel c compris entre a et b et tel que f(c) = g(c).
f(x) = exp(x)
g(x) = n-x

et comme tes deux fonction sont strictement monotones donc la solution est forcement unique

[marius1986]

bonjour, je dois démontrer que l'équation suivante admet une seule solution qu'on note



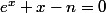
Il faut utiliser le théoreme des valeurs intermediares? Et donc montrer qu'elle est monotone ? J'ai aucune idee ...
merci!

Oui tu peux utiliser le théorème des valeurs intermédiaires.
En effet en posant tu montre que cette fonction est strictement croissante donc monotone et tu obtient immédiatement le résultat sur IR.

[ditans]

merci, et est ce que selon vous cest possible d'identifier Un ou tout du moins etudier sa convergence ?

[zerroudi]

quel convergence !
en prenant l'expression fn(x) donné par marius1986, il est facile de montrer :
1) lim fn(x) = +inf qd x tend vers +inf
2) lim fn(x) = -inf qd x tend vers -inf
3) la derivé de fn(x) = exp(x)+1 > 1 quelque soient x et n donc fn(x) strictement croissante


En conséquence, fn(x)=0 admet une solution unique

[kazeriahm]

on peut facilement montrer que U_n est croissante et qu'elle tend vers l'infini, pour avoir un equivalent il faut regarder en detail

[JJa]

Pour information :
une solution analytique de l'équation exp(x)-n+x=0 est exprimée grace à la fonction W(X) de Lambert avec X=exp(x):
x = n-W(exp(x))