Problème primitives et intégrales

[Leptune]

Bonjour à tous


Je passe le rattrapage demain, et j'ai quelques bloquages :

premièrement quelle est la primitive de e(-x) ? de e(x²) ?

Je trouve sur d'autres posts que cette dernière n'éxiste pas, ainsi , comment faire pour montrer que avecI=0S1 e(x²)dx 1<= I <= e

( ou 0S1 intégrale de O a 1 et <= infèrieur ou égal, histoire que ça puisse être clair pour tous. )


Et finalement, comment montrer que Un=0Sn x²e(-x)dx est croissante ?

merci d'avance a tous, puissent vos réponses être rapides ( je le passe demain a 13h30 ! ! )

Leptune.

[Maks]

Bonsoir !
Déjà, sais-tu ce qu'est une primitive d'une fonction ? La seule chose à retenir c'est que :
une primitive d'une fonction est une fonction avec .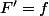
C'est tout !

Si tu retiens cette phrase, tout est simple !
Regarde :

Question : Quelle est une primitive de ? :hein:
Réponse : On peut penser dans un premier temps à .

Mais que vaut la dérivée de ? !

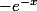Et si on prenait simplement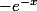 comme primitive ? Et là, miracle, en dérivant, on trouve bien ! :ptdr:

Est-ce que je suis assez clair ?

N'hésite pas à poser des questions ! Nous sommes là pour y répondre ! :id:

[Leptune]

Plus clair serait impossible !

Cette question faite, pourrais tu m'aider sur les autres qui a mon sens sont beaucoup plus problématiques : e(x²) a t-il une primitive ?

Comment faire pour cette intégrale avec des suites ?

Merci beaucoup de ta précieuse aide !

[girdav]

Bonsoir.
On a pour car la fonction est croissante sur cet intervalle.
On intègre entre et et on obtient le résultat.
Pour , on peut remarquer que la fonction à intégrer est positive ce qui montre que si on intègre sur un intervalle plus grand l'aire sous la courbe sera plus grande.

[Maks]

La question que tu me poses est en fait :
existe-t-il une fonction telle que ?
En fait, une telle fonction existe bien, mais tu ne pourras jamais l'expliciter, c'est-à-dire arriver à . C'est pour cela que dans les exercices, on utilise des procédés annexes pour prevoir un peu son comportement (par exemple, est-elle croissante ? est-elle positive ?). En se posant quelques questions de ce genre, et en utilisant des moyens détournés, on peut dans certains cas tracer le graphe de la fonction (mais tu n'auras toujours pas ).

J'espère que je suis toujours clair :marteau:

Donc au final, oui, la fonction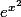 admet des primitives ! En fait, toutes les fonctions continues en admettent, et comme 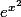est une fonction continue ...

Dis moi si tu suis jusque là.

[Leptune]

D'accord pour l'intégration, mais si il faut intégrer, il faut une primitive a e(x²), quelle est-t-elle ?


J'avoue par contre ne pas avoir très bien compris pour la suite, le raisonnement me parait logique, mais je ne vois pas du tout comment le mettre par écrit..

Merci d'avance

[Maks]

Non, on a pas besoin de la forme explicite de la primitive ! La seule chose qu'on utilise c'est que la fonction sous le signe intégrale est positive entre les bornes !

Regarde, ça devrait te paraître beaucoup plus clair :

Es-tu d'accord avec moi pour que l'intégrale d'une fonction, c'est globalement l'aire sous sa courbe ? (j'espère).
Ce qu'on dit c'est que :
-on ne connait pas la primitive (on ne peux pas donner l'aire sous la courbe en fonction des bornes)

MAIS

-on sait que la courbe est toujours au dessus de l'axe des abscisses !

DONC,

plus tu agrandis l'intervalle d'intégration, plus la valeur de l'intégrale augmente !
Facile, non ?

[girdav]

On ne fait que encadrer l'intégrale: ça évite de la calculer et ça permet de démontrer des trucs intéressants dessus.

[Leptune]

Je te suis, ainsi une fonction e(x²) admet des primitives mais que l'on ne pourra calculer, il faut donc résoudre l'intégrale par une étude de signe ?

[Leptune]

D'accord tout est bien claire a présent, et je vous en remercie.

Merci a vous deux.

[Maks]

Qu'entends-tu par "résoudre" l'intégrale ? Les méthodes annexes dont je t'ai parlé servent par exemple à dire que les primitives sont croissantes, qu'elles sont positives, qu'elles sont comprises entre telle valeur et telle valeur ...

Il arrive dans certains cas que tu puisses trouver la VALEUR de l'intégrale par des procédés annexes, mais pas toujours.

Tu n'est pas dans ce cas.

[busard_des_roseaux]

je passe le bac demain a 13h30 ! !

Leptune.

quelle est la primitive de e(x²) ?

Une fonction continue admet plusieurs primitives.
On doit dire "une primitive de f"

Révise ce qu'est une fonction strictement croissante:
une fonction strictement croissante est un morphisme d'ordre,
elle conserve les inégalités (sur un intervalle):


si a<b<c alors f(a)<f(b)<f(c)


La composée de deux fonctions strictement croissantes est strictement croissante:

exemple:
est strictement croissante sur l'intervalle

croissante sur l'intervalle

est strictement croissante sur


on en déduit que
si
alors

Les images étant comprises entre 1 et

on en déduit les mêmes inégalités pour les quadratures:

soit

Et finalement, comment montrer que
est croissante ?

Leptune.

nous changeons de variable. La fonction

est une intégrale sur le segment [0;x].
L'extrémité droite du segment est paramétrée.
On ne doit pas confondre cette borne avec la variable d'intégration qui,elle, varie dans l'intervalle

le cours dit que la fonction g de la variable x:


est une fonction dérivable , ayant pour fonction dérivée:



g,fonction à dérivée positive, est donc croissante sur l'intervalle

remarque:
une fonction peut être décroissante sur et
décroissante sur
sans être décroissante sur la réunion

par ex, et

Il faut donc parler de fonction croissante sur un intervalle et non pas
sur un domaine de définition non connexe

[Maks]

Bonjour, sans vouloir faire de critique non constructive, permets-moi de de te dire que je trouve que tu fais intervenir des notions loin du programme de terminale, et qu'au final, on passe à côté de l'essentiel.