Equation 2nd degré + limites

[chuchi]

et ensuite?? jte comprend po vraiment a vrai dire :--:

sinon pour la limite la prof a mit "on pour poser "

[CDuce]

Bon ce que je voulais dire c'est de remplacer i rac(3) par rac(3)e^i(Pi/2):

0+ i rac(3)= rac(3) (cos(Pi/2) + i sin (Pi/2) ) =[ rac(3),Pi/2]= rac(3)e^i(Pi/2) .
Tu n'a qu'a simplifier maintenant les e^.. pour ainsi trouver l'arg ici noté x chez toi c'est Alpha, et le module |z| des solutions .

Et pour la limite c'est juste X=1/x comme ça X tend vers O+ donc le tout vers +~ :)

[chuchi]

:marteau:

[CDuce]

Alors je recommence des le début ok :)
Bon avoir trouver les deux solutions Z1 et Z2 :
Prenons l'exemple de Z1:
Z1= [-e^-x + i rac(3) e^-x] / 2
= e^-x ( i rac(3) - 1 ) / 2
= -e^-x ( 1/2 - i rac(3) / 2 )
= -e^-x ( cos(Pi/6) - i sin(Pi/6) )
= -e^-x ( cos(-Pi/6) + i sin(-Pi/6) )

Or : ( cos(-Pi/6) + i sin(-Pi/6) ) = [1, -Pi/6 ]

[CDuce]

Donc je continue ;
[1, -Pi/6 ]= e^-Pi/6
Et - e^-Pi/6= e^(Pi-Pi/6)

alors : -e^-x * e^-Pi/6 = e^-x * -e^-Pi/6
= e^-x * e^(Pi-Pi/6)
= e^( 5Pi/6 - x )
Et voila donc :
|Z1|= 1
arg(Z1)= 5Pi/6 - x [2Pi] j'espère que je me suis bien expliquée ;)

[Billball]

Alors je recommence des le début ok
Bon avoir trouver les deux solutions Z1 et Z2 :
Prenons l'exemple de Z1:
Z1= [-e^-x + i rac(3) e^-x] / 2
= e^-x ( i rac(3) - 1 ) / 2
= -e^-x ( 1/2 - i rac(3) / 2 )
= -e^-x ( cos(Pi/6) - i sin(Pi/6) )
= -e^-x ( cos(-Pi/6) + i sin(-Pi/6) )

Or : ( cos(-Pi/6) + i sin(-Pi/6) ) = [1, -Pi/6 ]

ya un problème dans cqui a en rouge nan??!

je reprend cque j'avais au brouillon :




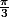
(cos + i sin )




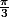
avec 1 > 0

soit |z1| = 1
arg z1 = -2pi/3 - [2pi]

ensuite



donc |z2| = | | = 1

arg z2 = arg = - arg z1 = - (2pi/3 - )
arg z2 = -2pi/3 +

ca devrait etre bon???

[chuchi]

Alors je recommence des le début ok
Bon avoir trouver les deux solutions Z1 et Z2 :
Prenons l'exemple de Z1:
Z1= [-e^-x + i rac(3) e^-x] / 2
= e^-x ( i rac(3) - 1 ) / 2
= -e^-x ( 1/2 - i rac(3) / 2 )
= -e^-x ( cos(Pi/6) - i sin(Pi/6) )
= -e^-x ( cos(-Pi/6) + i sin(-Pi/6) )

Or : ( cos(-Pi/6) + i sin(-Pi/6) ) = [1, -Pi/6 ]

ya un problème dans cqui a en rouge nan??!

je reprend cque j'avais au brouillon :




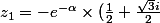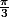
(cos + i sin )




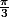
avec 1 > 0

soit |z1| = 1
arg z1 = -2pi/3 - [2pi]

ensuite



donc |z2| = | | = 1

arg z2 = arg = - arg z1 = - (2pi/3 - )
arg z2 = -2pi/3 +

ca devrait etre bon???

[CDuce]

Haa Désolé quelle faute mortelle :s:s c'est Pi/3 et non pas Pi/6 .
Sinon ce que t'as trouvé et juste :)

[chuchi]

jte remercie d'avoir pris le temps!!

[Timothé Lefebvre]

Bonsoir chuchi, ça ne te dérange pas de t'approprier les posts des autres (Billball ici) ?
Même s'ils sont effacés on les voit quand même ...

EDIT : oh, quelle surprise ! Multi-compte (identitifé par IP). Pour quelle(s) raison(s) ?

[CDuce]

Ce n'est rien ;)