Comparaison série - intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 23 Fév 2009, 09:37
par jeje56 » 23 Fév 2009, 09:37
Bonjour,
J'aimerais savoir si ma démarche est juste :
Je dois MQ

Je dis :
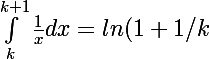\le 1/k)
pour tout k
D'où :

Merci bcp !
-
SimonB
 par SimonB » 23 Fév 2009, 10:44
par SimonB » 23 Fév 2009, 10:44
C'est juste, mais comment justifier ton inégalité
\leq \frac{1}{k})
?
Une manière plus simple est de ne pas intégrer et de se servir que, si f est une fonction décroissante, on a
toujours dx}\leq f(k))
(et de prouver ce fait).
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 23 Fév 2009, 11:13
par jeje56 » 23 Fév 2009, 11:13
SimonB a écrit:C'est juste, mais comment justifier ton inégalité
\leq \frac{1}{k})
?
Une étude de fonctions donne que pour tout x plus grand ou égal à -1, ln(1+x) inférieur ou égal à x... non ?
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 23 Fév 2009, 11:20
par Matt_01 » 23 Fév 2009, 11:20
jeje56 a écrit:Une étude de fonctions donne que pour tout x plus grand ou égal à -1, ln(1+x) inférieur ou égal à x... non ?
Oui oui c'est correct de cette manière, mais la deuxième méthode est bien plus rapide

-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 23 Fév 2009, 11:23
par jeje56 » 23 Fév 2009, 11:23
Ca marche, merci à vous deux ;-)
-
SimonB
 par SimonB » 23 Fév 2009, 11:46
par SimonB » 23 Fév 2009, 11:46
Matt_01 a écrit:Oui oui c'est correct de cette manière, mais la deuxième méthode est bien plus rapide

Et surtout susceptible de généralisations !
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 23 Fév 2009, 17:12
par Lierre Aeripz » 23 Fév 2009, 17:12
Il est quand même utile de se souvenir que le logarithme est une fonction concave, donc inférieure à toutes ses applications tangentes.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités