Espace tangent !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 13:35
par barbu23 » 11 Fév 2009, 13:35
Bonjour :
Définition :Soit :

une sous variété de :
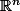
de classe :
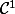
.
Soit :

Soit :

un vosinage ouvert de

.
Soit :

un vosinage ouvert de

.
Soit :

un :

- difféomorphisme tels que :
 = 0 $)
et
 = V \cap ( \mathbb{R}^{p} \times \{ 0 \} $)
.
Alors :
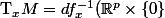 $)
.
Question :J'essaye de trouver un exemple concret qui illustre une application de cette définition, mais en vain ! Quelqu'un peut-t-il me donner un coup de pouce ?
Merci infiniment !
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 11 Fév 2009, 13:53
par ThSQ » 11 Fév 2009, 13:53
Regarde le cas n=p=1. Quelle est l'équation de la droite tangente ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Fév 2009, 14:03
par Doraki » 11 Fév 2009, 14:03
T'as pas une variété concrète M favorite et pas trop compliquée sur laquelle appliquer la définition ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 14:04
par barbu23 » 11 Fév 2009, 14:04
Dans le cas où :

: Les sous variétés de

se sont des intervalles.
Soit

un :
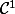
- difféomorphisme tel que :
 = 0 $)
et
 = ]c,d[ $)
Alors :

( Mais, il n'y'a pas un moyen de calculer explicitement :
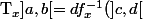 $)
Merci d'avance de vos réponse !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Fév 2009, 14:07
par Doraki » 11 Fév 2009, 14:07
Oui, là l'espace tangent c'est R.
Qu'est-ce que tu veux calculer explicitement ?_?
Il faut calculer l'image par

de

, pas de V.
Appliquer la définition pour trouver l'espace tangent ça te satisfait pas ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 14:08
par barbu23 » 11 Fév 2009, 14:08
Doraki a écrit:T'as pas une variété concrète M favorite et pas trop compliquée sur laquelle appliquer la définition ?
Hemm ... pas du tout ! :hum: :happy2:
Je pense au cercle décrit pas :

tel que :
 = ||x||_{2} $)
, mais
 \neq 0 $)
avec :

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 14:09
par barbu23 » 11 Fév 2009, 14:09
Doraki a écrit:Oui, là l'espace tangent c'est R.
Qu'est-ce que tu veux calculer explicitement ?_?
Il faut calculer l'image par

de

, pas de V.
Appliquer la définition pour trouver l'espace tangent ça te satisfait pas ?
 $)
?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 14:12
par barbu23 » 11 Fév 2009, 14:12
Doraki a écrit:Il faut calculer l'image par

de

, pas de V.
Appliquer la définition pour trouver l'espace tangent ça te satisfait pas ?
Non, relis entièrement la définition que j'ai écrit au debut de ce fil ! on cherche la préimage par rapport à un voisinage de

et non pas

tout entier ! c'est une condition je pense !
Merci d'avance de vos reponses !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 14:18
par barbu23 » 11 Fév 2009, 14:18
Ah d'accord, il faut chercher un exemple concret de

, par exemple :
 = x^{2} $)
pour savoir ce que ça donne ... !
 = 2x $)
et donc :
 = \mathbb{R} $)
Vos connaissez pas un autre exemple mais cette fois çi les applications sont définies dans des espaces de demension superieurs à

... pour povoir saisir mieux cette definition dans la tête !
Merci infiniment !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Fév 2009, 14:21
par Doraki » 11 Fév 2009, 14:21
barbu23 a écrit:Alors :

Pourquoi ?
C'est quoi tes M, U, V, et f que tu utilises pour la définition ?
Ce n'est pas ce que dit la définition, ça veut rien dire, à droite t'as un machin qui dépend de f alors que à gauche non.
Je saos pas si t'as lu ta définition, qui est bonne :
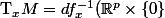 $)
Moi je vois un R^p là.
Je pense au cercle décrit par :

tel que :
 = ||x||_{2} $)
, mais
 \neq 0 $)
avec :

Rien compris à ta variété.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 14:32
par barbu23 » 11 Fév 2009, 14:32
Doraki a écrit:Pourquoi ?
C'est quoi tes M, U, V, et f que tu utilises pour la définition ?
Ce n'est pas ce que dit la définition, ça veut rien dire, à droite t'as un machin qui dépend de f alors que à gauche non.
Je saos pas si t'as lu ta définition, qui est bonne :
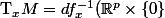 $)
Moi je vois un R^p là.
Rien compris à ta variété.
Les sous variétés

de
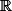
sont les intervalles de
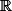
( n'est ce pas ? )

est un voisinage d'un point

de la variété

dans
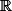

est un voisinage de

de
D'accord, pour la deuxième remarque !
Pour la dernière, tu m'a dit : T'as pas une variété concrète M favorite et pas trop compliquée sur laquelle appliquer la définition ?, j't'ai repondu que la seule que j'ai dans la tête est :
 = ||x||_{2} = 1 $)
avec

définie sur un cercle

... mais, elle est partout non nulle sur le cercle ( donc, elle n'est pas comme ce qu'il y'a dans la definition qui exige que
 = 0 $)
Amicalement !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 14:34
par barbu23 » 11 Fév 2009, 14:34
Vous connaissez pas un autre exemple mais cette fois çi les applications sont définies dans des espaces de demensions superieurs à 2 ... pour pouvoir saisir mieux cette definition dans la tête !
Merci infiniment !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Fév 2009, 14:52
par Doraki » 11 Fév 2009, 14:52
Les sous variétés de R sont les ouverts de R.
Sinon pour ton cercle, t'es vraiment pas clair.
Tu peux utiliser le paramétrage polaire du plan :
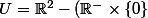\\<br />V = ]-\pi ; +\pi[ \times ]-1 ; +\infty[)
f : (x,y) -> (la mesure de l'argument de x+iy dans ]-pi;+pi[ , ||x,y|| - 1)
f est une bijection de U sur V, et envoie U inter S1 dans V inter (R * {0})
Après ça t'as plus qu'à calculer la différentielle de f, vérifier que c'est un difféomorphisme C1, et choisir un point dans U inter S1 pour voir ce que ça donne.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 15:08
par barbu23 » 11 Fév 2009, 15:08
Merci Doraki pour ces precisions ! :++:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 15:16
par barbu23 » 11 Fév 2009, 15:16
Pour l'argument de

c'est
 $)
( n'est ce pas ? ) et
||_{2} - 1 = x^{2}+y^{2} - 1 $)
Donc :
 = ( \arctan (\frac{y}{x}) , x^{2}+y^{2}-1) $)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 15:27
par barbu23 » 11 Fév 2009, 15:27
Soit :


}}{\partial x} & \frac{\partial {\arctan (\frac{y}{x})}}{\partial y} \\ \frac{\partial {(x^{2}+y^{2}-1)}}{\partial x} & \frac{\partial {(x^{2}+y^{2}-1)}}{\partial y} \end{pmatrix} \begin{pmatrix} h_{1} \\ h_{2} \end{pmatrix} = \begin{pmatrix} \frac{-y}{x^{2}+y^{2}} & \frac{x}{x^{2}+y^{2}} \\ 2x & 2y \end{pmatrix} \begin{pmatrix} h_{1} \\ h_{2} \end{pmatrix} $)
N'est ce pas Doraki ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 15:36
par barbu23 » 11 Fév 2009, 15:36
J'ai preque fini tout le boulot, mais j'arrive pas à conclure ! Quelqu'un peut-t-il m'aider ?
Merci infiniment !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 15:41
par barbu23 » 11 Fév 2009, 15:41
Le determinant de la matrice Jacobienne est égale à :

, donc inversible, donc :

est linaire bijective, continue d'inverse continue, dérivable d'inverse derivable, de dérivée continue ... donc, c'est un difféomorphisme de classe
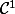
... ! Et pour la suite , comment on fait ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Fév 2009, 15:44
par barbu23 » 11 Fév 2009, 15:44
C'est quoi alors :
} \mathbb{S} $)
par exemple ?
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
 par R.C. » 11 Fév 2009, 16:10
par R.C. » 11 Fév 2009, 16:10
Bonjour,
barbu23 a écrit:C'est quoi alors :
} \mathbb{S} $)
par exemple ?
et bien tu "n'as plus qu'à" remplacer (x,y) par
)
dans ta matrice, à l'inverser, puis à calculer l'image de (0,1).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
de
, pas de V.
tel que :
, mais
avec :