Base d'un espace tangent à une variété !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 25 Jan 2009, 15:36
Bonjour :
Soit
_{i\in I}) $)
une variété différentiable de dimension :
.
Soit :
les fonctions de changement de cartes.
Soit :
avec :
fixé .
Notons :
 = P' $)
et donc :
=y(x(P)) $)
.
Je voudrai savoir comment on obtient la formle suivante ( avec la notation d'Einstein ) :
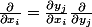
Ils disent que c'est par dérivée de la composé de deux applications, mais je ne vois pas encore comment la demontrer !
Merci infiniment !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 25 Jan 2009, 17:32
Aidez moi svp ! Merci d'avance !
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
par Maxmau » 25 Jan 2009, 20:17
Bj
Quelle est la dérivée de la fonction t ----- > f(x(t),y(t),z(t)) ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 25 Jan 2009, 23:22
Salut "Maxmau" et mercçi pour la réponse !
J'ai trouvé pourquoi :
Daprès le calcul de la dérivée dune fonction composée :
tel que :
^{k} = \frac{\partial f^{j}}{\partial x^{i}} . \frac{\partial g^{k} }{\partial y^{j}} $)
i.e :
=J_g . J_f $)
(
: matrice Jacobienne )
i.e :
Merci quant même pour la reponse !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 25 Jan 2009, 23:25
J'ai une autre question à vous poser :
Pourquoi :
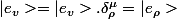
Pour la première égalité : ça va, pour l'autre, je ne vois pas encore d'où ça vient !
désigne une application linéaire de
( e.v. ) vers
( e.v. )
est la base canonique de
,
est la base duale de
 $)
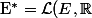Merci d'avance de votre aide !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
