DM super compliqué!!

[Timothé Lefebvre]

Bonsoir, même pas la dérivée ni le tableau ?

[Mithos]

je vais réfléchir à tout ça, si je trouve je t'aide, mais je n'ai pas un super niveau alors bon...

mais je ne t'abandonne pas ^^

[Mithos]

Comme tu as l'air de vraiment galérer, je te fais les limites.

EDIT : supprimé par la modération, pas les solutions ...


Pour alphan, tu dis que g est continue (car dérivable) en ]-infini ; +infini[ et qu'elle est strictement croissante. g(]-infini ; +infini[) = ]-infini ; +infini[. 0 apparient à cet intervalle donc l'équation g(x)=0 admet une unique solution alphan (là je dis la rédac, la solution étant évidente).

Bon, voilà le tout pour démarrer ton devoir, la suite essaie de la faire tout seul, si tu y arrives vraiment pas je m'y pencherai ^^

[Mithos]

c'est ça.

Effectivement je suis allé trop vite en t'affirmant qu'elle était strictement croissante.

En réalité la dérivée est e^x(2+x), ce qui fait qu'elle est du signe de 2+x.
Donc ce n'est pas les intervalles ]-infini;0[ et ]0;-infini[ qui sont concernés mais... à toi de trouver, on a pas le droit de donner les réponses j'ai cru comprendre.

[Mithos]

je dois m'absenter, mais je reviens dans 30-60 minutes

[Mithos]

Me revoilà,

Je me suis penché sur la question 4)a. et j'avoue ne pas voir comment faire... Je vais poursuivre mes recherches.

Vu ce que je viens de dire, je ne file pas mon MSN, en revanche si il me vient à trouver subitement plusieurs solutions, je veux bien ^^

[xyz1975]

Lorsqu'un individu dans la rue te demande : comment montrer que 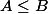, tu réponds par : Il suffit de considérer la différence puis examiner le signe de cette dérnière quitte à étudier des variations lorsqu'il s'agit de fonctions :
Pour montrer que :
Tu peux tout simplement considérer la fonction puis étudier ses variations pour en déduire le signe.

[xyz1975]

ah c'te spa sbete du tout ça!!!

Je comprends pas ce que tu dis, pas de sms ici!!!

[xyz1975]

Mais attends regarde:
h(x)=ln(x)-(x+1)
=ln(x)-x+1
donc h'(x)=1/x -1
du coup, pour x>0, on a pas toujours lnx inférieur ou égale à x-1, vu qu'il y a le -1 dans l'expression de h'(x) non?

Mais je t'ai demandé d'étudier les variations ce qui signifie le signe de h'(x).
Tu as comme x est supposé strictement positif alors :
h'(x) est positive si et seulement si 1-x l'est soit x plus petit que 1.
h'(x) est négative si et seulement si 1-x l'est soit x plus grand que 1.
par conséquence :
h est croissante sur ]0;1] et est décroissante sur [1;+00[
Traces un tableau de variation de h et regarde la valeur maximale de cette fonction c'est bien 0 ce qui montre qu'elle est négative, c'est bien ce qu'on cherche à prouver.