Famille Libres Bases ... [MPSI]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 14:54
par Antho07 » 30 Déc 2008, 14:54
Tu as fais comment la 2 ??
Pour la 4 , on écrit
= \bigsum_{k=1}^{n} \alpha_{k} P_{k}(X))
La question est combien vaut
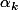
Que donne
Ce polynome si on l'évalue en

(le Ak present dans les definitions des Pk )
(raaa les a ressemblent à des alphas....)
-
Ulcan
- Membre Naturel
- Messages: 38
- Enregistré le: 13 Avr 2008, 16:34
-
 par Ulcan » 30 Déc 2008, 15:07
par Ulcan » 30 Déc 2008, 15:07
Alors pour la 2) ce que j'ai fait j'ai dit que
Soit i un entier naturel compris entre 1 et n-1
Deg(Pi)on a donc n-1 polynôme d dégrées distincts donc forcément les coefficients sont nuls
Par contre l'évaluation des Ak je ne vois pas du tout
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 15:15
par Antho07 » 30 Déc 2008, 15:15
sauf que
deg(P1)=deg(P2)=Deg(P3) =2 (dans le cas où n=3)
Les polynomes Pk sont tous de degré n-1
On ne peut pas utiliser le degré ici.
On va faire autrement ici.
Je rappelle que

sont n reels
distinctset qu'on definit pour tout k entre 1 et n
=\bigprod_{i=1 \\ i \neq k }^{n} (X -A_{i}))
On veut montrer la liberté de la famille
 , \ldots , P_{n}(X))
Méthode habituelle, on prend une combinaison linéaire nulle des vecteurs de cette famille.
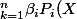 =0)
avec

.
Il faut montrer qu'alors les beta sont tous nuls.
Question intermédiaire (qui servira aussi pour la question 4).
Que vaut
)
si
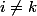
?
-
Ulcan
- Membre Naturel
- Messages: 38
- Enregistré le: 13 Avr 2008, 16:34
-
 par Ulcan » 30 Déc 2008, 15:19
par Ulcan » 30 Déc 2008, 15:19
Pk ( Ai) ça représente pour toi
Pk(Ai) = Pi ( 1 à Ai Ai différent de i) (X-Ai)?
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 15:22
par Antho07 » 30 Déc 2008, 15:22
Ulcan a écrit:ça ne fait pas 0
Puis que i différent de k on aura jamais ( Ai-Ai)?
Tu as pas répondu à la bonne question:
On aura effectivement
 \neq 0 \, \forall k)
parce que
dans Pk(X) , le facteur (X-Ak) n'apparait pas et comme les A1,...,An sont distintcs , le produit Pk(Ak) est donc non nul.
Maintenant, on fixe k
on prend un i différent de k
Combien vaut
)
?
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 15:25
par Antho07 » 30 Déc 2008, 15:25
Ulcan a écrit:Pk ( Ai) ça représente pour toi
Pk(Ai) = Pi ( 1 à Ai Ai différent de i) (X-Ai)?
non , on garde les notations
= \bigprod_{i=1 \\ i \neq k }^{n} (X-A_{i}))
On evalue en
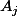
(pour pas se faire des noueds dans les notation. On fixe un j different de k )
=\bigprod_{i=1 \\ i \neq k }^{n} (A_{j}-A_{i}))
Comme si on avait P(X)=X^3+X
alors P(2)=2^3+2
-
Ulcan
- Membre Naturel
- Messages: 38
- Enregistré le: 13 Avr 2008, 16:34
-
 par Ulcan » 30 Déc 2008, 15:29
par Ulcan » 30 Déc 2008, 15:29
je pense que ça fera 0 parce qu'il y'aura un moment ou on aura Ai=Aj?
puisqu'"il n'est pas dit que j différent de i
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 15:36
par Antho07 » 30 Déc 2008, 15:36
J'ai n réels

J'ai n polynomes:
, \ldots P_{n}(X))
Je prend un polynome :
Je fixe un k entre 1 et n et je prends
)
(le k est fixé il bouge plus)
Maintenant , je prends un j entre 1 et n différent de k
et je prend le réel
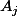
qui corréspond.
J'ai un polynome
)
et un réel
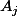
.
Les constantes k et j sont fixés , elles ne bougent plus à partir de maintenant .
Combien vaut
=\bigprod_{i=1 \\ i \neq k} ^{n} (A_{j}-A_{i}) =(A_{j}-A_{1}) \times \ldots \times (A_{j}-A_{k-1}) \times (A_{j}-A_{k+1}) \times \ldots \times (A_{j}-A_{n}))
sachant que k est different de j
-
Ulcan
- Membre Naturel
- Messages: 38
- Enregistré le: 13 Avr 2008, 16:34
-
 par Ulcan » 30 Déc 2008, 15:40
par Ulcan » 30 Déc 2008, 15:40
Dans ce cas là je ne vois plus mais ça peut faire 0
ok k différent de j mais peut être que k-1 = j donc comme c'est un produit 0*c*a*r =0 quand même .
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 15:41
par Antho07 » 30 Déc 2008, 15:41
Ulcan a écrit:je pense que ça fera 0 parce qu'il y'aura un moment ou on aura Ai=Aj?
puisqu'"il n'est pas dit que j différent de i
voilà c'est ça.
Les polynomes
, \ldots, P_{n} (X))
vérifient
 \neq 0)
si j=k ( donc si l'indice du polynome est le meme que l'indice du A)
 =0)
si

(si l'indice du polynome est different de l'indice du A)
Maintenant on revient à la combinaison linéaire
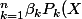 =0)
Je fixe un p entre 1 et n et j'evalue tout ça en Ap
Cela donne
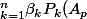 =0(A_{p})=0)
Mais a gauche on peut simplifier (ya des termes de la sommes qui sont nuls)
Qu'est-ce qui reste apres simplifications?
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 15:44
par Antho07 » 30 Déc 2008, 15:44
Ulcan a écrit:Dans ce cas là je ne vois plus mais ça peut faire 0
ok k différent de j mais peut être que k-1 = j donc comme c'est un produit 0*c*a*r =0 quand même .
Oui le polynome Pk(X)
est le produit de tous les (X-Ai) sauf (X-Ak)
Donc si on evalue en un j different de k
(X-Aj) etant un facteur de Pk(X) cela fait 0
Si on evalue en Ak
(X-Ak) ne fait pas partie des facteurs de Pk(X) (le seul qui n'en fait pas partie) donc comme les A1...An sont distincts
Pk(Ak) est non nul
-
Ulcan
- Membre Naturel
- Messages: 38
- Enregistré le: 13 Avr 2008, 16:34
-
 par Ulcan » 30 Déc 2008, 15:49
par Ulcan » 30 Déc 2008, 15:49
Quand on a p=1 ou p-1=i etc... on aura des Pk(Ap) nuls
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 15:57
par Antho07 » 30 Déc 2008, 15:57
(X- Ap) divise tous les Pk(X) sauf Pp(X)
Donc
Pk(Ap)=0 pour tout k sauf pour k=p
donc
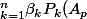\\=\beta_{1} P_{1}(A_{p})+\ldots +\beta_{p-1}P_{p-1}(A_{p})+\beta_{p} P_{p}(A_{p})+\beta_{p+1}P_{p+1}(A_{p+1})+\ldots+ \beta_{n} P_{n}(A_{p})\\=0+\ldots+0+\beta_{p}P_{p}(A_{p})+0 +\ldots+0)
donc finalement la combinaison lineaire devient
=0)
(quand on l'evalue pour Ap (p entre 1 et n))
Maintenant,
 \neq 0)
On en déduit que

et on peut faire ça pour tous les p entre 1 et n.
=> les beta sont tous nuls et la famille est libre
-
Ulcan
- Membre Naturel
- Messages: 38
- Enregistré le: 13 Avr 2008, 16:34
-
 par Ulcan » 30 Déc 2008, 16:20
par Ulcan » 30 Déc 2008, 16:20
Merci beaucoup pour cette question
Je vais réfléchir sur la 4) et je vous tiendrais au courant merci encore
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 16:25
par Antho07 » 30 Déc 2008, 16:25
Ulcan a écrit:Merci beaucoup pour cette question
Je vais réfléchir sur la 4) et je vous tiendrais au courant merci encore
La 4 c'est exactement le meme raisonnement
-
Ulcan
- Membre Naturel
- Messages: 38
- Enregistré le: 13 Avr 2008, 16:34
-
 par Ulcan » 30 Déc 2008, 16:32
par Ulcan » 30 Déc 2008, 16:32
Ah oui c'est bon j'ai trouvé la 4) c plus la somme = 0 mais la somme = p donc ça roule tout seule :) merci encore
je réfléchit pour la 5) et je vous tiens au courant
-
Ulcan
- Membre Naturel
- Messages: 38
- Enregistré le: 13 Avr 2008, 16:34
-
 par Ulcan » 30 Déc 2008, 19:45
par Ulcan » 30 Déc 2008, 19:45
Bon bah je ne trouve pas la question numero 5 ) j'ai beau à cherhcer je ne trouve pas:s
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 30 Déc 2008, 21:31
par Antho07 » 30 Déc 2008, 21:31
Les polynomes
 ,\ldots, P_{n}(X))
conviennent presque, ils vérifient 0 quand il faut.
Le seul probleme c'est que
 \neq 1)
Cela etant remarqué,
Soit p entre 1 et n:
on veut un polynome
)
qui vaut 1 en Ap et 0 sur tous les autres Aj
Pp(X) n'est pas très éloigné de celui ci, il faut juste le diviser par un coéfficient tels que
=1)
On posera alors
 =\frac{1}{\beta_{p}}P_{p}(X))
et on aura gagné
il faut trouver ce

On veut
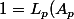=\frac{P_{p}(A_{p})}{\alpha_{p}})
soit finalement
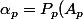=\bigprod_{i=1 \\i \neq p}^{n} (A_{p}-A_{i}))
donc finalement
=\frac{1}{\bigprod_{i=1 \\ i \neq p}^{n}(A_{p}-A_{i})}{\bigprod_{i=1 \\ i \neq p }^{n} (X-A_{i})} \\ =\bigprod_{i=1 \\ i\neq p}^{n} \frac{X-A_{i}}{A_{p}-A_{i}})
On definit les L1(X) .... Ln(X) comme ceci.
On vérifie qu'ils sont libres (de la meme maniere que la question 2).
On appele ces polynomes les polynomes de base d'interpolation de Lagrange.
(d'ou le L)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités