Salut, voilà un petit problème qui me pose quelques difficultés:
Calculer la valeur exacte de :
1+cos(2pi/5)+cos(4pi/5)+cos(6pi/5)+cos(8pi/5)
Merci d'avance...
Exercice Terminale S
5 messages
- Page 1 sur 1
Bonjour,
On sait que cos(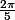 )=
)=
et comme cos(2a)=2cos²a-1
alors cos(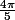 )=2(
)=2( )²-1 =-
)²-1 =-
Pour cos(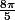 ) tu fais la même chose et tu trouves
) tu fais la même chose et tu trouves  .
.
Et pour cos(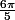 ) tu utilises une formule d'addition et tu trouves -
) tu utilises une formule d'addition et tu trouves - .
.
Après tu additionnes le tout et tu trouves 0.
À mon avis on n'avait pas pas besoin de faire de calcul si c'est pour trouver ce résultat, alors je vais chercher une méthode plus simple.
On sait que cos(
et comme cos(2a)=2cos²a-1
alors cos(
Pour cos(
Et pour cos(
Après tu additionnes le tout et tu trouves 0.
À mon avis on n'avait pas pas besoin de faire de calcul si c'est pour trouver ce résultat, alors je vais chercher une méthode plus simple.
cos(2*Pi/5) = (-1 + sqrt(5))/4
C'est évident... tout le monde le connaît par coeur...
Pour retrouver ce résultat :
posons x = 2*Pi/5
on cherche donc cos(x)
on sait que cos(5*x) = cos(2*Pi) = 1
on développe cos(5*x) :
cos(5*x) = Re(cos(5*x) + i*sin(5*x)) = Re((cos(x) + i*sin(x))^5)
je ne détaille pas les calculs... bref, on obtient cos(5*x) = P(cos(x)) une expression polynomiale du type a5*cos(x)^5 + ... + a1*cos(x) + a0
donc a5*cos(x)^5 + ... + a1*cos(x) + (a0 - 1) = 0
cos(x) est donc une solution X de a5*X^5 + ... + a1*X + (a0 - 1) = 0 telle que -1 < X < 1 ou plutôt 0 < X < 1
C'est évident... tout le monde le connaît par coeur...
Pour retrouver ce résultat :
posons x = 2*Pi/5
on cherche donc cos(x)
on sait que cos(5*x) = cos(2*Pi) = 1
on développe cos(5*x) :
cos(5*x) = Re(cos(5*x) + i*sin(5*x)) = Re((cos(x) + i*sin(x))^5)
je ne détaille pas les calculs... bref, on obtient cos(5*x) = P(cos(x)) une expression polynomiale du type a5*cos(x)^5 + ... + a1*cos(x) + a0
donc a5*cos(x)^5 + ... + a1*cos(x) + (a0 - 1) = 0
cos(x) est donc une solution X de a5*X^5 + ... + a1*X + (a0 - 1) = 0 telle que -1 < X < 1 ou plutôt 0 < X < 1
1+cos(2pi/5)+cos(4pi/5)+cos(6pi/5)+cos(8pi/5)
salut
tout cela vaut SOM(2.k.pi/5) pour k compris entre 0 et 4.
on sait de plus que cox =(e^ix+e^-ix)/2
en, posant x=2k.pi/5 et en effectuant la somme membre à membre
pour k compris entre 0 et 4 on arrive au résultat en prenant ensuite la partie réelle du résultat.
a+
salut
tout cela vaut SOM(2.k.pi/5) pour k compris entre 0 et 4.
on sait de plus que cox =(e^ix+e^-ix)/2
en, posant x=2k.pi/5 et en effectuant la somme membre à membre
pour k compris entre 0 et 4 on arrive au résultat en prenant ensuite la partie réelle du résultat.
a+
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
