Problème Tle S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:04
par Antho07 » 10 Nov 2008, 22:04
titlana a écrit:je suis perdu :briques:
oublie le message de nierh si il te dit rien, on en a pas vraiment besoin
on a trouvé une fonction qui vérifie f'=3f mais pas f(-1)=2
pour l'instant on a f(-1)=e^(-3)
Il va falloir transformer un peu notre fonction
Il va falloir forcer le f(-1)=2 en modifiant la fonction f (sans changer la dérivée)
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:08
par Antho07 » 10 Nov 2008, 22:08
Une solution pourrait etre de se dire.
Bon la fonction qu'on a a les bonnes variations(f'=3f) , mais elle passe a la bonne hauteur pour x=-1. Peu importe, translatons là pour qu'elle passe à la bonne hauteur.
Comment on translate une courbe?
-
titlana
- Membre Naturel
- Messages: 17
- Enregistré le: 10 Nov 2008, 21:02
-
 par titlana » 10 Nov 2008, 22:10
par titlana » 10 Nov 2008, 22:10
Il fau faire un truc du genre f(-1)= e(-3) + p ?
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:12
par Antho07 » 10 Nov 2008, 22:12
titlana a écrit:Il fau faire un truc du genre f(-1)= e(-3) + p ?
exactement.
il faut qu'on ait :
f(-1)=2
On a pour l'instant
f(-1)=e(-3)
bon ben translatons la courbe de 2-e(-3).
Donc finalement f(x)=.... ?
-
Neirh
- Membre Naturel
- Messages: 18
- Enregistré le: 10 Nov 2008, 20:55
-
 par Neirh » 10 Nov 2008, 22:12
par Neirh » 10 Nov 2008, 22:12
Ptit bidouilleur !!!
Mais j'aime bien
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:19
par Antho07 » 10 Nov 2008, 22:19
STOOOOOOOOOOOOOOOOOOOP
arretons tous je me suis emballe cela marche pas du tout.
J'ai oublie le probleme initiale entre temps.
Pourquoi cela marche pas, parce que si on translate on modifie l'ordonnée et le la fonction e^(3x) +2-e(-3) ne verifie plus f'=3f
je suis sincerement désolé je repost dans 30s
-
titlana
- Membre Naturel
- Messages: 17
- Enregistré le: 10 Nov 2008, 21:02
-
 par titlana » 10 Nov 2008, 22:21
par titlana » 10 Nov 2008, 22:21
je me disais aussi je n'y arrivais pas c'est pas grave je réfléchi encore ^^
-
Neirh
- Membre Naturel
- Messages: 18
- Enregistré le: 10 Nov 2008, 20:55
-
 par Neirh » 10 Nov 2008, 22:21
par Neirh » 10 Nov 2008, 22:21
Je me suis armé d'un crayon est en effet,
C'était trop facil, :hum: , c'était pourtant une idée originale
Je pensais à ça quand je pensais à plusieurs solutions :triste:
Faut reprendre
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:22
par Antho07 » 10 Nov 2008, 22:22
Bon alors encore désolé pour l'erreur.
On va travailler sur la fonction
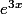
, cela ça change pas.
Cependant il faut se debrouiller pour transformer la fonction de sorte que
f(-1)=2, mais il faut que les transformation qu'on fait sur f soit egalement faite sur f' pour conserver f'=3f.
Comment faire alors?
bon on a vu que si on chercher a faire des additions ou soustraction cela marchait pas.
Quelle operation a des chances de marcher alors?
-
titlana
- Membre Naturel
- Messages: 17
- Enregistré le: 10 Nov 2008, 21:02
-
 par titlana » 10 Nov 2008, 22:24
par titlana » 10 Nov 2008, 22:24
division ? :hein:
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:27
par Antho07 » 10 Nov 2008, 22:27
titlana a écrit:division ? :hein:
exacte division ou multiplication par une constante non nul ne posera pas de probleme.
En effet si f verifie f'=3f
alors pour a non nul
la fonction af verifira encore l'equation
Preuve:
(af)'(x)=af'(x)=a3f(x)=3af(x)=3(af(x))
Donc maintenant on cherche la solution sous la forme:
=ae^{3x})
que vaut a?
-
Neirh
- Membre Naturel
- Messages: 18
- Enregistré le: 10 Nov 2008, 20:55
-
 par Neirh » 10 Nov 2008, 22:27
par Neirh » 10 Nov 2008, 22:27
entre autre,
continue
pose un reel qui vérifie l'équation (que tu aura trouvé ;)
-
Neirh
- Membre Naturel
- Messages: 18
- Enregistré le: 10 Nov 2008, 20:55
-
 par Neirh » 10 Nov 2008, 22:29
par Neirh » 10 Nov 2008, 22:29
Bizarre, l'équation que tu propose me dit vaguement quelque chose, non?? :we:
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:31
par Antho07 » 10 Nov 2008, 22:31
Neirh a écrit:Bizarre, l'équation que tu propose me dit vaguement quelque chose, non??
oui oui , evidemment les solutions des equations différentielle lineaire du premiere ordre sans second membre , yen a pas 36000 mais vu que les equas diff n'ont pas encore ete faite... il faut se debrouiller autrement
-
titlana
- Membre Naturel
- Messages: 17
- Enregistré le: 10 Nov 2008, 21:02
-
 par titlana » 10 Nov 2008, 22:33
par titlana » 10 Nov 2008, 22:33
a= e(-3) /2 ?
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:35
par Antho07 » 10 Nov 2008, 22:35
titlana a écrit:a= e(-3) /2 ?
si on pose
=\frac{e^{-3}}{2}e^{3x})
comme tu le suggère, alors
=\frac{e^{-3}}{2}e^{-3})
cela n'a pas l'air d'être cela.
-
Neirh
- Membre Naturel
- Messages: 18
- Enregistré le: 10 Nov 2008, 20:55
-
 par Neirh » 10 Nov 2008, 22:36
par Neirh » 10 Nov 2008, 22:36
Par division, c'est ça,
tu peut vérifier la dérivé si tu veux
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:39
par Antho07 » 10 Nov 2008, 22:39
Bon comme tu l'auras trouvé la fonction recherchée est
=\frac{2}{e^{-3}}e^{3x})
-
titlana
- Membre Naturel
- Messages: 17
- Enregistré le: 10 Nov 2008, 21:02
-
 par titlana » 10 Nov 2008, 22:39
par titlana » 10 Nov 2008, 22:39
je ne vois pas du tou jai besoin d'être éclairer :hein:
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 10 Nov 2008, 22:41
par Antho07 » 10 Nov 2008, 22:41
titlana a écrit:je ne vois pas du tou jai besoin d'être éclairer :hein:
tu t'etais juste plantée de sens pour le a
on a f(x)=ae(-3x)
on veut f(-1)=2
soit
ae(-3)=2 donc a =2/e(-3) et non pas e(-3)/2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
