Problème Tle S

[titlana]

bOnsoir je suis en terminale S et j'ai un probléme je n'arrive pas à résoudre cet exercice : Derterminer l'équation d'une courbe passant par A(-1;2) et telle qu'en chaque point le coeff dir de la tangente soit le triple de l'ordonnée du point

Voila je vous remercie d'avance il me faudrait une réponse avant mercredi

[Antho07]

Bonsoir peut etre traduire tout cela sous forme d'equation d'abord

[titlana]

je sais que le coeff dir de la tan à la courbe en un point c'est le nombre f'(x) donc si le coeff directeur de la tan est le triple de l'ordonnée du point c'est que f'(x)=3f(x) pour aprés je vois pas :hum:

[Antho07]

je sais que le coeff dir de la tan à la courbe en un point c'est le nombre f'(x) donc si le coeff directeur de la tan est le triple de l'ordonnée du point c'est que f'(x)=3f(x) pour aprés je vois pas :hum:

ok jusque là, c'est bon.

As-tu vu les equations différentielles?

[titlana]

non pas encore

[Neirh]

Salut,
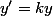
L'écriture : ne te dit rien? :id:
C'est une équation differentielle,
à toi de la résoudre

[titlana]

ah si effectivement je vais tenter ^^

[Antho07]

D'accord bon, heu normalement tu as vu la fonction exponentielle?

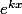
Je crois qu'il y a un truc sur les fonctions , non?


EDIT: oublie ce post si tu as vu les equa diff

[titlana]

bon en fait je n'ai pas fait les equations différentielles
bref dans mon cours e(kx) apparait uniquement dans ce théoréme : Il existe une unique fonction f dérivable sur R telle que f'=kf et f(0)=1 telle que pour tout x appartenant a R f(x)=e(kx)

[Antho07]

bon en fait je n'ai pas fait les equations différentielles
bref dans mon cours e(kx) apparait uniquement dans ce théoréme : Il existe une unique fonction f dérivable sur R telle que f'=kf et f(0)=1 telle que pour tout x appartenant a R f(x)=e(kx)

bon si on pose alors




on est pas très loin de la solution.

Qu'est ce qui reste à faire?

[titlana]

On remplace k par 3 mais ça revien a ce que javais di au dessus f'(x) =3f nn ?

[Neirh]

Il manque pas une donnée dans l'énoncé,
Je trouve plusieurs solutions,
Je l'ai pas ecrit mais graphiquement, je m'imagine plein de courbes differentes
:doh:

[titlana]

L'énoncé est complet

[Antho07]

On remplace k par 3 mais ça revien a ce que javais di au dessus f'(x) =3f nn ?

oui c'est pour cela que j'ai dit vu qu'on connait une fonction qui vérifie f'=3f

on a qu'a prendre cette fonction là

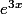
(donc ) puis maintenant il va falloir la bidouiller un peu pour répondre correctement à l'énoncé.


Qu'est ce qui manque pour que la fonction satisfasse les données de l'ennoncé?

[titlana]

il faut qu'elle passe pas A(-1;2)

[Antho07]

il faut qu'elle passe pas A(-1;2)

oui donc faut que f(-1)=2

Combien vaut f(-1) ?

si

[titlana]

f(-1)=e(-3) nn ? :hein:

[Antho07]

f(-1)=e(-3) nn ? :hein:

oue donc on a pas gagné encore

Il faudrait se démerder pour que f(-1)=2.

Qu'est ce qu'on pourrait faire?

[Neirh]

Désolé, je me suis embrouillé,
Quoi qu'il en soit, il n'y aurait pas un second théorème où l'on dit :
?

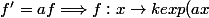[titlana]

je suis perdu :briques: