Spé maths : : probléme de congruence.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Disco
- Messages: 3
- Enregistré le: 11 Oct 2008, 18:06
-
 par Disco » 04 Nov 2008, 13:27
par Disco » 04 Nov 2008, 13:27
Bonjour je bute sur une partie d'un DM de spé :
-2- Soit a un entier naturel non divisible par 7
a) montrer que a^0 congru à 1 modulo 7 (ca ca va)
b) On appelle ordre de a modulo 7 et on designe par k le plus petit entier naturek non nul tel que a^k congru a 1 modulo 7
Montrer que le reste de r de la division euclidienne de 6 par k verifie a^r congru a 1 modulo 7
Si r different de 0, montrer que l'on aboutit à une contradiction. en deduire que k divise 6
Quelles sont les valeurs possible de k ?Voila j'aurai besoin de conseils pour la partie en gras

Merci d'avance
-
Disco
- Messages: 3
- Enregistré le: 11 Oct 2008, 18:06
-
 par Disco » 04 Nov 2008, 19:08
par Disco » 04 Nov 2008, 19:08
up :) j'ai toujours pas reussi
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 04 Nov 2008, 19:18
par lapras » 04 Nov 2008, 19:18
salut,
montre que

(soit par récurrence mais c'est lourd, soit par factorisation :
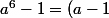(a+1)(a^2+a+1)(a^2-a+1))
:happy2:
Ecris ce que te demandes l'énoncé :
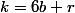
et
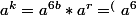^b*a^r=...=1 [7])
Il faut aussi se rappeller que k est le plus
petit entier non nul vérifiant

-
Disco
- Messages: 3
- Enregistré le: 11 Oct 2008, 18:06
-
 par Disco » 05 Nov 2008, 11:47
par Disco » 05 Nov 2008, 11:47
soit par factorisation : a^6-1 = (a-1)(a+1)(a^2+a+1)(a^2-a+1)
Tu peux develloper stp ? je ne comprends ^pas quoi faire de cette expression.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
