Exercice sur les suites (TS)
15 messages
- Page 1 sur 1
Exercice sur les suites (TS)
Bonsoir,
Je vous remercie d'avance pour le temps que vous passerez à lire et a répondre si possible à mon message.
J'ai l'exercice suivant à faire et je ne parviens vraiment pas à le résoudre le voici :
Démontrer, à l'aide d'un raisonnement par récurrence que pour tout n e N (ensemble des entiers naturels), il existe deux entiers naturels an et bn tels que :
( 2 + ;)3)^n = an + bn x ;)3
Je ne vois meme pas comment faire pour initialiser car j'ai fais le premier membre élevé a la puissance 0 et j'obtiens 1 mais je ne m'occupe pas de mon second membre ce qui je pense n'est pas normal.
Merci encore
Je vous remercie d'avance pour le temps que vous passerez à lire et a répondre si possible à mon message.
J'ai l'exercice suivant à faire et je ne parviens vraiment pas à le résoudre le voici :
Démontrer, à l'aide d'un raisonnement par récurrence que pour tout n e N (ensemble des entiers naturels), il existe deux entiers naturels an et bn tels que :
( 2 + ;)3)^n = an + bn x ;)3
Je ne vois meme pas comment faire pour initialiser car j'ai fais le premier membre élevé a la puissance 0 et j'obtiens 1 mais je ne m'occupe pas de mon second membre ce qui je pense n'est pas normal.
Merci encore
sur les suites (TS)
Bonsoir,
sans donner la réponse, voici beaucoup de détails qui devraient vous permettre de conconclure:
On initialise avec et
et 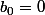
pour ,
, ^{1}) =
= donc
donc 
et
pour ,
, ^{2}) =
=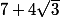 =
=
donc et
et 
...
l'hérédité c'est il existe deux suites) et
et ) tel
tel
que^{n}=a_{n}+b_{n}\sqrt{3})
ensuite on calcule
^{n+1}) en écrivant
en écrivant
^{n+1}=(2+\sqrt{3})^{n}(2+\sqrt{3})) =
=(2+\sqrt{3}))
en développant on obtient et
et 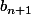 en fonction de
en fonction de
 ,
, 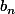 et
et 
il n'a plus qu'à faire les calculs.
Bonne rédaction.
sans donner la réponse, voici beaucoup de détails qui devraient vous permettre de conconclure:
On initialise avec
pour
et
pour
donc
...
l'hérédité c'est il existe deux suites
que
ensuite on calcule
en développant on obtient
il n'a plus qu'à faire les calculs.
Bonne rédaction.
Merci à vous deux,
J'ai encore une question quand tu fais (2+ racine de 3) ^n+1 dans ton égalité tu n'aurais pas oublié avec an et bn la racine de 3 ?
Pour moi on obtient:
(2+ racine de 3) ^n+1 = (an + bn x racine de 3) x (2+racine de 3) ?
Je vois peut etre pas le truc excuse moi...
Et ensuite faut il faire n+1 - n ?
Ce qui donnerait (2+ racine de 3)^n+1 - (2+racine de 3) ^n
Merci d'avance
J'ai encore une question quand tu fais (2+ racine de 3) ^n+1 dans ton égalité tu n'aurais pas oublié avec an et bn la racine de 3 ?
Pour moi on obtient:
(2+ racine de 3) ^n+1 = (an + bn x racine de 3) x (2+racine de 3) ?
Je vois peut etre pas le truc excuse moi...
Et ensuite faut il faire n+1 - n ?
Ce qui donnerait (2+ racine de 3)^n+1 - (2+racine de 3) ^n
Merci d'avance
Je ne sais pas ce que je veux mais j'ai du mal sur ce chapitre et en m'aidant avec d'autres exercices je vois qu'à chaque fois avec l'initialisation on doit vérifier la propriété avec n+1 et on fait souvent n+1 - n d'où mon calcul que j'ai exposé précédement.
Donc en gros je ne dois pas le faire c'est bien ça ?
Donc en gros je ne dois pas le faire c'est bien ça ?
sur les suites (TS)
Bonjour,
C'est juste il manque

On a bien
^{n+1}=(2+\sqrt{3})^{n}(2+\sqrt{3})=(a_{n}+b_{n}\sqrt{3})(2+\sqrt{3})=(2a_{n}+3b_{n})+(a_{n}+2b_{n})\sqrt{3})
)
En posant et
et 
Les suites) et
et ) existent car on a pu les définir par récurrence.
existent car on a pu les définir par récurrence.
La réponse est-elle claire?
C'est juste il manque
On a bien
En posant
Les suites
La réponse est-elle claire?
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
