Sens de Variation

[pmloik]

Bonjours je voudrai avoir une petite aide pour cette exercice.

On considère les fonctions f et g définies sur R par:

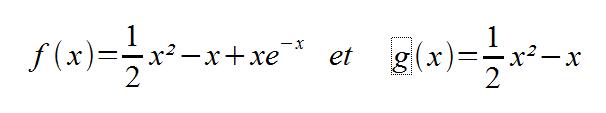
On notera Cf et Cg les courbes représentatives de ces fonctions dans un repère orthonormal (unité graphique: 2cm)
f(x) peut s'écrire sous la forme:

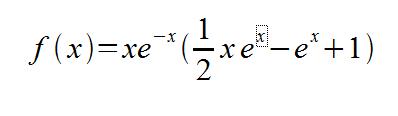
1/a) Calculer la dérivée f' de f.
Montrer que pour tout nombre réel x:
f'(x)=(x-1)(1-e^-x).
b) Etudier le signe de f'(x).
c) Dresser le tableau de variations de f.

2/ Donner le tableau de variations de g.
3/ Tracer Cf et Cg

[rene38]

Bonjour

Ressemble beaucoup à [url="http://www.maths-forum.com/showthread.php?t=70367"]ça[/url].

[pmloik]

Oui en fait ça c'est la 2eme partie de l'exercice

[pmloik]

Je suis désolé de ne pas avoir mis les 2 ensembles.
Mais tu pourrais m'aider pour mon exercice s'il te plait ?

[rene38]

Quest-ce qui t'arrête ?

Tu as calculé f '(x) ?

[pmloik]

Oui mais je trouve un résultat autre que celui donné

[pmloik]

c'est bon ça ?

[rene38]

c'est bon ça ?

Non : u est aussi un produit donc u' ...
de même le premier terme de v

Un conseil : utilise plutôt l'écriture de f(x) donnée au début : le calcul est plus simple.

[pmloik]

Mais si je prend celle la je doit utiliser quelle formule ?

[pmloik]

c'est bon ?

[rene38]

Tu n'as absolument rien changé !

[pmloik]

Si j'ai marqué f'(x)=x-1+e^(-x)
mais je sais pas si on le voit

[rene38]

Reprenons : et dérivons chaque terme :
dérivée de =...
dérivée de = ...
dérivé de = ...
d'où

[pmloik]

dérivée de (1/2)x²=1x
-x=1
xe^-x=1e^-x

[rene38]

-x=1 sors le - de ta poche !


xe^-x=1e^-x Non est un produit : utilise (uv)'=u'v+uv'

[pmloik]

ça fait e^(-x)+xe^(-x) nan ?

[rene38]

Toujours pas : la dérivée de n'est pas

[pmloik]

c'est e^(x) ?

[pmloik]

donc ça fait e^(-x)+xe^(x) bon?

[rene38]

c'est e^(x) ?

Non : on a affaire à une fonction composée et tu dois avoir vu que si k est une fonction, la dérivée de est