Systeme lineaire

[olivia83]

J'ai un probleme pour résoudre un systeme lineaire

2x+3y+z=6
x+2y-z=0
-3x-5y+z= -1

Comment m'y prendre svp

[leon1789]

En te servant de la seconde équation, élimine les x des 2 autres équations : ainsi tu vas obtenir 2 (nouvelles) équations à (seulement) 2 inconnues y et z....

[oscar]

Bonjour


Tu peux éliminer facilement les "z"

[olivia83]

merci j'ai trouvé =)

J'ai encore un probleme car j'ai trois equation à deux inconnues et ce ne sont pas les même

x+2z=0
y-3z=0
3x+2y=0

[andros06]

Slt , en repartant du système énoncé

(Eq1 = équation n°1)

Eq1 + Eq2 : 3x+y=6
Eq2 + Eq3 : -2x-3y=-1

D'où x = ... et y = ...

Eq1 : z = 6 -2x -3y donc z = ...

ps : ça devrait pas plutôt se situer dans la partie "Lycée" ce message ?

[olivia83]

Pour mon deuxieme probleme :
J'ai trouvé 0 mais je ne suis pas sur que cela soit la seule solution.
Car si on sort x et y des deux premieres equations, et qu'on les remplace dans la 3eme equation, on peut voir que celle ci verifie la 3eme equation.

Cela ne veut pas dire qu'il y a une infinité de solution?

[leon1789]

Cela ne veut pas dire qu'il y a une infinité de solution?

oui : donc la troisième équation est inutile à rien.

3 inconnues, 2 équations indépendantes : l'ensemble solution est une droite...

[olivia83]

je comprend pas pourquoi c'est une droite

[kaya]

Salut à tous
Juste un ptit problème: je sais pas faire une réduction de Jordan
J'ai déjà plein de cours mais j'arrive pas trop à comprendre. Je demande de l'aide.
Ce serait sympa si vous me guidiez dans un site où je pourrais trouver des corrigés (avec toutes les démarches à suivre bien sur).
Sinon j'éssaie de réduire cette matrice en réduite de Jordan:



J'ai trouver:
-Polynôme caractéristique :
-Polynôme minimale :

Merci et A+

[mathelot]

salut,

On additionne les trois égalités, ça donne: z=5.

les deux premières égalités donne le système 2x2 de déterminant 1:




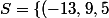on vérifie la solution trouvée sur les 3 égalités du système initial.