Module et argument (surement facile :D)

[Florix]

Bonsoir,

J'ai posté y'a pas longtemps, où je le résultat suivant :



On m'a ensuite mis "Le module et l'argument sont alors faciles à calculer"

Ben oui mais moi je sais pas comment on fait !

Si quelqu'un pouvait m'aider ! Parait que c'est super simple !

Merci d'avance

[Chimerade]

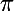
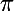
L'argument du produit d'un réel A positif par un complexe Z est égal à l'argument de Z. L'argument du produit d'un réel A négatif par un complexe Z est égal à l'argument de Z + . 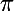La règle générale est que l'argument du produit de deux complexes est égal à la somme des arguments des deux facteurs ; comme l'argument d'un réel est 0 ou , dans le cas d'un réel, l'argument du produit d'un réel par un complexe est donc tout simplement égal à l'argument du complexe si le réel est positif, à la somme de l'argument du complexe et de , si le réel est négatif.

Quant au module, le module d'un produit est le produit des modules.


puisque
si est positif
si est négatif