Conique

[mostdu95]

bonsoir
soit M un point de la parabole de foyer F et de directrice D distinct du sommet o .montrer que la tangente en M est la bissectrice intérieure de l'angle FMH
en fait j'ai trouvé l'equation de la tangente qui est :(si Y=2pX l'eqt de la parabole et soit M(x0,y0)sur la parab la tg a pour equt:yy0=p(x+x0)px+y0y=px0 )
mais j'arrive pas à prouver que c'est la bissectrice de FMH
aidez moi et merci d'avance

[abcd22]

Bonsoir,
Le triangle FMH est isocèle en M d'après la définition avec directrice et foyer d'une parabole, donc la bissectrice de l'angle FMH est aussi la médiane issue de M de ce triangle...
L'équation que tu donnes pour la tangente n'est pas très claire...

[mostdu95]

MERSI D'ABORD POUR VOTRE REPONSE
MAIS ce n'est pas ça : yy0=p(x+x0) ou px+y0y=px0 ??l'equation de la tangente

[abcd22]

L'équation de la parabole est f(x,y) = y² - 2px = 0, l'équation de la tangente en un point de la courbe est (c'est une conséquence du théorème des fonctions implicites), ce qui donne ici . Si on fait les calculs en écrivant 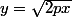ou 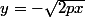(tu as dû faire ça puisque tu donnes 2 équations de tangentes ?) on doit retrouver la même chose.

[mostdu95]

d'accord et comment on conclut apres avoir l'expression de la tangente??

[abcd22]

J'ai dit plus haut que la bissectrice était la médiane issue de M du triangle FMH, donc on peut essayer de montrer que la tangente est aussi cette médiane...

[mostdu95]

et comment vous arrivez à montrer que la tangente c'est la meme que la mediane .....??
en fait j'ai trouvé une autre methode dans un livre mais la votre me semble la plus stylée :++: c'est pour ça que j'aimerai bien savoir comment vous concluez associer la mediane a la tangente a part de chercher encore l'equation de la mediane et là....!!!ouf

[abcd22]

La médiane c'est la droite qui passe par M et par le milieu I du segment [FH], la tangente passe par M, il reste à calculer les coordonnées de I et montrer que I est sur la tangente.